
【题目】太阳能热水器的玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最佳.如图,某户根据本地区冬至时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光与玻璃吸热管垂直).已知:支架CF=100 cm,CD=20 cm,FE⊥AD于E,若θ=37°,求EF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
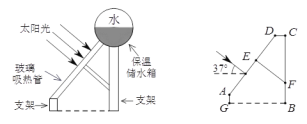
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】给出下面四个命题,其中真命题的个数有( )
(1)平分弦的直径垂直于这条弦,并且平分这条弦所对的弧;
(2)90°的圆周角所对的弦是直径;
(3)在同圆或等圆中,圆心角的度数是圆周角的度数的两倍;
(4)如下图,顺次连接圆的任意两条直径的端点,所得的四边形一定是矩形.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
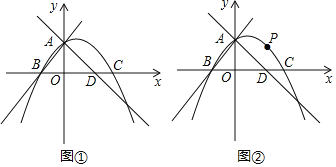
【题目】如图①,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转90°,所得直线与
逆时针旋转90°,所得直线与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)如图②,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点
上方抛物线上的一个动点
①当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标和最大距离;
的坐标和最大距离;
②当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y =-x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB, 抛物线y =ax2+bx+4经过A,B,C三点.
OB, 抛物线y =ax2+bx+4经过A,B,C三点.
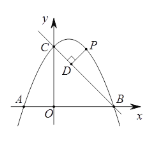
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值;
(3)设点E为抛物线对称轴与直线BC的交点,若A,B,E三点到同一直线的距离分别是d1,d2,d3,问是否存在直线l,使得d1= d2=![]() d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
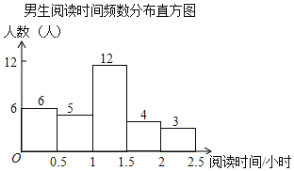
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )

A.  B.
B. 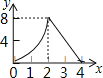
C. 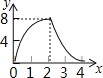 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李白笔下“孤帆一片日边来”描述了在喷薄而出的红日映衬下,远远望见一叶帆船驶来的壮美河山之境.聪明的小芬同学利用几何图形,构造出了此意境!如图半径为5的⊙0在线段AB上方,且圆心O在线段AB的中垂线上,到AB的距离为![]() ,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=
,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=![]() ,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )
,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com