
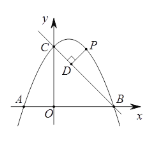
【题目】如图,直线y =-x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB, 抛物线y =ax2+bx+4经过A,B,C三点.
OB, 抛物线y =ax2+bx+4经过A,B,C三点.
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值;
(3)设点E为抛物线对称轴与直线BC的交点,若A,B,E三点到同一直线的距离分别是d1,d2,d3,问是否存在直线l,使得d1= d2=![]() d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
【答案】(1)y=-![]() x2+ x+4;(2)当m=2时,PE最大,最大值为
x2+ x+4;(2)当m=2时,PE最大,最大值为![]() ;(3)存在,满足题意的d3的值为2或6或
;(3)存在,满足题意的d3的值为2或6或![]() .
.
【解析】
(1)由直线y=-x+4得出B(4,0),C(0,4),即可得出A(-2,0),将A与B坐标代入抛物线解析式求出a与b的值,即可确定出抛物线解析式;
(2)已知P点横坐标,根据直线AB、抛物线的解析式,求出C、P的坐标,由此得到线段PC的长;在Rt△OBC中,∠OCB=45°,根据平行线的性质得出∠PFD=45°,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
(3)见解析.
解:(1)由y=-x+4得 当x=0时,y=4; 当y=0时,x=4.
∴ B(4,0) , C(0,4), ∴ OB=4.
∴ OA=![]() OB=2, ∴ 点 A(-2,0).
OB=2, ∴ 点 A(-2,0).
把A(-2,0),B(4,0)分别代入抛物线y=ax2+bx+4中,得
![]() 解得
解得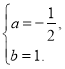
∴ 抛物线的解析式为 y=-![]() x2+ x+4.
x2+ x+4.
(2)∵ 点P的横坐标为m,则P(m,-![]() m2+ m+4).
m2+ m+4).
过点P作PF∥y轴交BC于点F,则F(m,-m+4) .
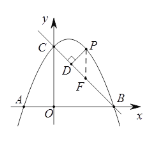
∴ PF=-![]() m2+ m+4-(-m+4)=-
m2+ m+4-(-m+4)=-![]() m2+2m.
m2+2m.
在Rt△OBC中,OB=4,OC=4.
又 PF∥y轴, ∴ ∠PFD=∠OCB=45°.
∴ PD=PF·sin∠PFD= PF·sin∠OCB =![]() (-
(-![]() m2+2m)=-img src="http://thumb.zyjl.cn/questionBank/Upload/2020/10/22/06/64e53364/SYS202010220603483477190214_DA/SYS202010220603483477190214_DA.008.png" width="28" height="45" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />(m-2)2+
m2+2m)=-img src="http://thumb.zyjl.cn/questionBank/Upload/2020/10/22/06/64e53364/SYS202010220603483477190214_DA/SYS202010220603483477190214_DA.008.png" width="28" height="45" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />(m-2)2+![]() .
.
∵ 0<m<4,-![]() <0,∴ 当m=2时,PE最大,最大值为
<0,∴ 当m=2时,PE最大,最大值为![]() .
.
(3)存在,∵y=-![]() x2+ x+4=-
x2+ x+4=-![]() (x-1)+
(x-1)+![]() ,
,
∴C点坐标为(1,3),
如图,d1= d2=![]() d3 ,
d3 ,
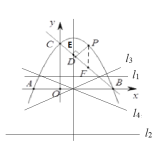
满足题意的d3的值为2或6或![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
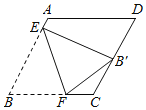
【题目】在菱形ABCD中,AB=2,∠BAD=120°,点E,F分别是边AB,BC边上的动点,沿EF折叠△BEF,使点B的对应点B’始终落在边CD上,则A、E两点之间的最大距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能热水器的玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最佳.如图,某户根据本地区冬至时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光与玻璃吸热管垂直).已知:支架CF=100 cm,CD=20 cm,FE⊥AD于E,若θ=37°,求EF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
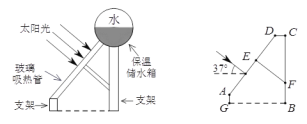
查看答案和解析>>
科目:初中数学 来源: 题型:
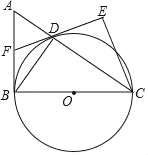
【题目】如图,已知直角△ABC中,∠ABC=90°,BC为圆O的直径,D为圆O与斜边AC的交点,DE为圆O的切线,DE交AB于F,且CE⊥DE.
(1)求证:CA平分∠ECB;
(2)若DE=3,CE=4,求AB的长;
(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
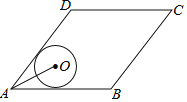
【题目】如图,菱形ABCD的边AB=5,面积为20,∠BAD<90°,⊙O与边AB、AD都相切,AO=2,则⊙O的半径长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,潘老师给出如下定义:如果一个三角形有一边上的高线等于这条边的一半,那么称这个三角形为“垂美三角形”,这条边称为这个三角形的“垂美边”.
概念理解:
(1)如图①,已知∠A=90°,AB=AC,请证明等腰Rt△ABC一定是“垂美三角形”.
探索运用:
(2)已知等腰△ABC是“垂美三角形”,请求出顶角的度数.
能力提升:
(3)如图②,在直角坐标系中,点A为x轴正半轴上动点,在反比例函数![]() 的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com