
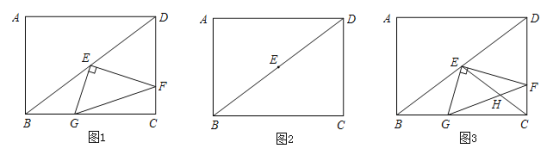
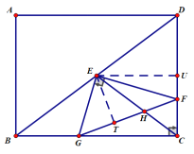
����Ŀ����ͼ1���ھ���ABCD�У�AB=6��BC=8����E�ǶԽ���BD���е㣬ֱ�ǡ�GEF����ֱ�DZ�EF��EG�ֱ�CD��BC�ڵ�F��G��
��1������F�DZ�CD���е㣬��EG�ij���
��2����ֱ�ǡ�GEF��ֱ�Ƕ���E��ת����ת���������CD��BC���ڵ�F��G����EFG�Ĵ�С�Ƿ����仯������仯����˵�����ɣ�������䣬�����tan��EFG��ֵ��
��3����ֱ�ǡ�GEF�ƶ���E��ת����ת���������CD��BC���ڵ�ֱ�߽��ڵ�F��G����ͼ2�л���ͼ�Σ����жϡ�EFG�Ĵ�С�Ƿ����仯������仯����˵�����ɣ�������䣬��ֱ��д��tan��EFG��ֵ��
��4����ͼ3������CE��FG�ڵ�H����![]() �������CF�ij���
�������CF�ij���
���𰸡���1��EG=3����2�����䣬 tan��EFG=![]() ����3�����仯��tan��EFG=
����3�����仯��tan��EFG=![]() ����4��
����4��![]() ��
��
��������
(1)���ݵ�E�ǶԽ��ߵ��е㣬��F��CD���е㣬��֤EF��BC���ٸ�����GEF=90������C=90���ɵ��ı���EGCFΪ���Σ����G��BC���е㣬��ɽ��EG�ij���
��2����EM��CD��M��EN��BC��N���þ���ENCM����֤����GEN�ס�FEM������
![]() ������tan��EFG=
������tan��EFG=![]() ������EFG���仯��
������EFG���仯��
(3)����ͼ�Σ����գ�2���з������̣����ɵó���EFG���仯����tan��EFG=![]() ��
��
(4) ��E�ֱ���ET��GF��T��EU��CD��U����tan��EFG=![]() ����EG=3a��EF=4a��
����EG=3a��EF=4a��
��GF=5a��ET=![]() ��GT=
��GT=![]() ����
����![]() �����FH=
�����FH=![]() ��GH=
��GH=![]() �������ֱ����EH��CH�ij�����֤��FHC�צ�EHG����
�������ֱ����EH��CH�ij�����֤��FHC�צ�EHG����![]() ���ɴ����aֵ�������ֱ�EF��UF�ij����������CF�ij�.
���ɴ����aֵ�������ֱ�EF��UF�ij����������CF�ij�.
��1����E��FΪBD��CD���е�
��EF��BCD�����
��EF=![]() BC=4�� EF��BC
BC=4�� EF��BC
������ABCD����C=90��
���EFC=90��
�ߡ�GEF=90��
���ı���EGCFΪ����
��EG=FC=![]() =3��
=3��
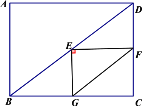
��2�����仯��
��ͼ����EM��CD��M��EN��BC��N���þ���ENCM��
���NEM=90��
�ߡ�GEF=90��
���GEN=��FEM
���GEN�ס�FEM
��![]()
�� tan��EFG=![]() ��
��
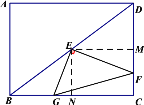
��3����ͼ��ʾ�����仯��tan��EFG=![]() ;
;

���ɣ���EM��CD��M��EN��BC��N���þ���ENCM��
���NEM=90��
�ߡ�GEF=90��
���GEN=��FEM���֡�ENG=��EMF=90��
���GEN�ס�FEM
��![]()
�� tan��EFG=![]() ��
��
(4)��E�ֱ���ET��GF��T��EU��CD��U��
��tan��EFG=![]() ����GEF=90��
����GEF=90��
�ʿ���EG=3a��EF=4a��
��GF=5a��ET=![]() ��GT=
��GT=![]() ��
��
��![]() ��
��
��FH=![]() ��GH=
��GH=![]() ��
��
��HT=GH-GT=![]() -
-![]() =
=![]() ��
��
��EH=![]() =
=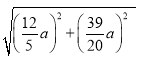 =
=![]() ��
��
�ߡ�BCD=90��BC=8��AB=CD=6��
��BD=10����E��BD���е㣬
��CE=![]() BD=5��
BD=5��
��CH=CE-EH=5-![]() ��
��
��tan��CE=![]() ��tan��EGF=
��tan��EGF=![]() ��
��
���UCE=��EGF������CHF=��EHG��
�তFHC�צ�EHG��
��![]() ����
����![]() ��
��
��![]() ��(5-
��(5-![]() )=
)=![]() ��
��![]() ��
��
��![]() ��
��
��EF=![]() ��
��
��UF=![]() =
=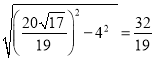 ��
��
��CF=CU-UF=3-![]() =
=![]() .
.


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
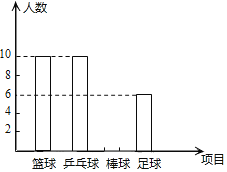
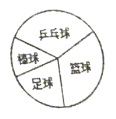
����Ŀ��Ϊ�˽�ij������ѧ��һ�ܿ����Ķ�ʱ��������������ȡ������ѧ�����е��飬���ݵ����������Ķ�ʱ����Ϊ���ࣺ2Сʱ���ڣ�2��4Сʱ����2Сʱ����4��6Сʱ����4Сʱ����6Сʱ�����ϣ�����������ͼ��ʾ�в�������ͳ��ͼ��
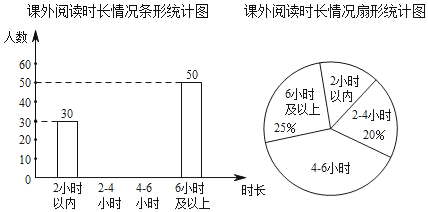
��1�����ε��鹲�����ȡ���� ������ѧ�������п����Ķ�ʱ����2��4Сʱ�������� ���ˣ�
��2������ͳ��ͼ�У������Ķ�ʱ����4��6Сʱ����Ӧ��Բ�ĽǶ���Ϊ�� ���㣻
��3�����õ�������20000����ѧ�������Ƹõ�����ѧ��һ�ܿ����Ķ�ʱ��������4Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ƽ��ı�����.���ſƼ��ķ�չ���Զ����̶�Խ��Խ�ߣ��������г�Խ��Խ��.ij�̳�����һ��![]() ��
��![]() ����Ʒ�Ƶı�̻����ˣ����۷ֱ�Ϊÿ̨3000Ԫ��4000Ԫ.�г����鷢�֣�����3��
����Ʒ�Ƶı�̻����ˣ����۷ֱ�Ϊÿ̨3000Ԫ��4000Ԫ.�г����鷢�֣�����3��![]() Ʒ�ƻ����˺�2��
Ʒ�ƻ����˺�2��![]() Ʒ�ƻ����ˣ��ɻ�����6000Ԫ������2��
Ʒ�ƻ����ˣ��ɻ�����6000Ԫ������2��![]() Ʒ�ƻ����˺�3��
Ʒ�ƻ����˺�3��![]() Ʒ�ƻ����ˣ��ɻ�����6500Ԫ.
Ʒ�ƻ����ˣ��ɻ�����6500Ԫ.
��1�����̳�![]() .
.![]() ����Ʒ�Ƶı�̻��������ۼ۸�ֱ��Ƕ���Ԫ��
����Ʒ�Ƶı�̻��������ۼ۸�ֱ��Ƕ���Ԫ��
��2�����̳����ò�����65000Ԫ���ʽ�![]() ��
��![]() ����Ʒ�Ƶı�̻����˹�20������������Ҫ����
����Ʒ�Ƶı�̻����˹�20������������Ҫ����![]() Ʒ�Ƶı�̻����˶��ٸ���
Ʒ�Ƶı�̻����˶��ٸ���
��3���������������أ��̳�����![]() Ʒ�Ʊ�̻���������������
Ʒ�Ʊ�̻���������������![]() Ʒ�Ʊ�̻�����������
Ʒ�Ʊ�̻�����������![]() ���ִ��㹺��
���ִ��㹺��![]() ��
��![]() ����Ʒ�Ʊ�̻����˹�40���������������ܻ����������
����Ʒ�Ʊ�̻����˹�40���������������ܻ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=x+4��ͼ���뷴��������y=![]() ��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��1����˷����������ı���ʽ��
��2������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
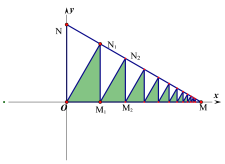
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��![]() ����������ֱ���M��N���㣬����O��
����������ֱ���M��N���㣬����O��![]() ����
����![]() ��
��![]() ������Ӱ
������Ӱ![]() ���ٹ�
���ٹ�![]() ��
��![]() ����
����![]() ��
��![]() ������Ӱ
������Ӱ![]() ��������˽�����ȥ����õ���������Ӱ�����ε����֮��Ϊ_________��
��������˽�����ȥ����õ���������Ӱ�����ε����֮��Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ḻͬѧ�ǵ�У���ijУ������չ�������ࡢ�����ࡢ�Ļ������ʽ���������Ż��ÿ�˽��μ�һ�������ʦ�ھ��꼶�����ȡ��2���༶������2���༶�μ����������Ż���������������ͳ�ƣ��������������ͳ��ͼ����֪��2���༶����![]() ��ѧ���μӡ�������Ŀ��������ͳ��ͼ�С�������Ŀ����Բ�Ľ�Ϊ
��ѧ���μӡ�������Ŀ��������ͳ��ͼ�С�������Ŀ����Բ�Ľ�Ϊ![]() ��
��
��1����2����μ����������Ż����Ϊ______��
��2������ͼ�н���ʾ��������Ŀ��ͼ�β���������
��3������У���꼶����600��ѧ�����������������Ϣ���Ƹ�У���꼶���ж�����ѧ���μӡ�������Ŀ��
��4��С����С�ն�����2�����ѧ�����Ҷ��μ������������Ż�������б�����״ͼ����С����С�ն��μ��������ŵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʻС�������ٵش�A����ʹ��B�أ���ʻ���Ϊ480ǧ�ף���С��������ʹʱ��Ϊt����λ��Сʱ������ʹ�ٶ�Ϊv����λ��ǧ��/Сʱ������ȫ���ٶ���Ϊ������120ǧ��/Сʱ.
����v����t�ĺ�������ʽ��
�Ʒ�������8���ʻС������A����.
�ٷ������ڵ���12��48����14�㣨��12��48�ֺ�14�㣩�䵽��B�أ���С������ʻ�ٶ�v�ķ�Χ.
�ڷ����ܷ��ڵ���11��30��ǰ����B�أ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������![]() ��k��0����ͼ����һ�κ���y=-x+b��ͼ���ڵ�һ������A��B���㣬BC��x���ڵ�C������OBC�����Ϊ2����A���������Ϊ4��B���������Ϊ1��
��k��0����ͼ����һ�κ���y=-x+b��ͼ���ڵ�һ������A��B���㣬BC��x���ڵ�C������OBC�����Ϊ2����A���������Ϊ4��B���������Ϊ1��
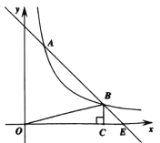
��1������������һ�κ����ı���ʽ��ֱ��AB��x�ύ��E�����ꣻ
��2����֪��D��t��0����t��0��������D����ֱ��x���ֱ�ߣ��ڵ�һ��������һ�κ���y=-x+b��ͼ���ཻ�ڵ�P���뷴�Ⱥ���![]() �ϵ�ͼ���ཻ�ڵ�Q������Pλ�ڵ�Q���Ϸ������Ϻ���ͼ��ֱ��д����ʱt��ȡֵ��Χ��
�ϵ�ͼ���ཻ�ڵ�Q������Pλ�ڵ�Q���Ϸ������Ϻ���ͼ��ֱ��д����ʱt��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
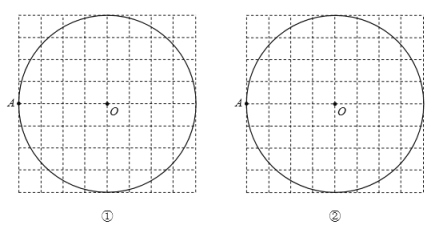
����Ŀ����ͼ��������ֽ�У�![]() ��
��![]() ���Ǹ�㣬��
���Ǹ�㣬��![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ�����̶ȵ�ֱ��������»�ͼ������д������
Ϊ�뾶��Բ�����̶ȵ�ֱ��������»�ͼ������д������
��1����Բ���л�Բ![]() ��һ���ڽ���������
��һ���ڽ���������![]() ��
��
��2����ͼ���л�Բ![]() ��һ���ڽ����˱���
��һ���ڽ����˱���![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com