
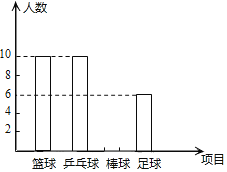
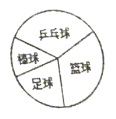
【题目】为丰富同学们的校园生活,某校积极开展了体育类、文艺类、文化类等形式多样的社团活动(每人仅限参加一项).李老师在九年级随机抽取了2个班级,对这2个班级参加体育类社团活动的人数情况进行了统计,并绘制了下面的统计图.已知这2个班级共有![]() 的学生参加“足球”项目,且扇形统计图中“足球”项目扇形圆心角为
的学生参加“足球”项目,且扇形统计图中“足球”项目扇形圆心角为![]() .
.
(1)这2个班参加体育类社团活动人数为______;
(2)请在图中将表示“棒球”项目的图形补充完整;
(3)若该校九年级共有600名学生,请你根据上述信息估计该校九年级共有多少名学生参加“棒球”项目?
(4)小明和小刚都是这2个班的学生,且都参加了体育类社团活动,请用列表或树状图法求小明和小刚都参加足球社团的概率.
【答案】(1)30;(2)补充图见解析;(3)24名;(4)![]()
【解析】
(1)依据扇形统计图中“足球”项目扇形圆心角为![]() ,可得出参加“足球”项目的学生数占参加体育类社团活动学生数的百分比,从而可得到这2个班参加体育类社团活动人数;
,可得出参加“足球”项目的学生数占参加体育类社团活动学生数的百分比,从而可得到这2个班参加体育类社团活动人数;
(2)利用参加体育类社团活动的总人数减去参加“篮球”项目,“乒乓球”项目以及“足球”项目的人数,可得出参加“棒球”项目的人数,即可将图形补充完整;
(3)根据这2个班级参加“足球”项目的人数以及其所占的百分比可得出这2个班的总人数,再依据参加“棒球”项目的人数占这2个班总人数的百分比,即可估计该校九年级参加“棒球”项目的学生人数;
(4)根据题意列表或画出树状图,然后得出总的情况数以及小明和小刚都参加足球社团的情况数,根据概率公式得出结果即可.
解:(1)这2个班参加体育类社团活动人数为:6÷![]() =30(人),
=30(人),
故答案为:30.
(2)参加“棒球”项目的人数为:30-10-10-6=4(人),
如图所示: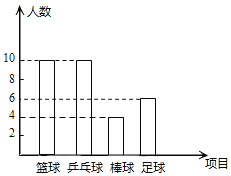
(3)6÷6%=100(人),![]() (人).
(人).
答:估计该校九年级共有24名学生参加“棒球”项目.
(4)画树状图如下:

由树状图可知共有16种结果,其中小明和小刚都参加足球社团有1种情况,
∴小明和小刚都参加足球社团的概率为![]() .
.


科目:初中数学 来源: 题型:
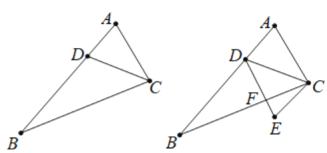
【题目】如图1,在△ABC中,D是AB上一点,已知AC=10,AC2=AD·AB.
(1)证明△ACD∽△ABC.
(2)如图2,过点C作CE∥AB,且CE=6,连结DE交BC于点F;
①若四边形ADEC是平行四边形,求![]() 的值;
的值;
②设AD=x,![]() =y,求y关于x的函数表达式.
=y,求y关于x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
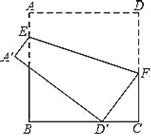
【题目】如图,正方形![]() 的边长是9,点
的边长是9,点![]() 是
是![]() 边上的一个动点,点
边上的一个动点,点![]() 是
是![]() 边上一点,
边上一点,![]() ,连接
,连接![]() ,把正方形
,把正方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
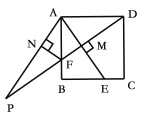
【题目】如图,正方形ABCD中,点E为BC边上的一点,连接AE,过点D作DM⊥AE,垂足为点M,交AB于点F.将△AMF沿AB翻折得到△ANF.延长DM,AN交于点P. 给出以下结论①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() ;.其中正确的是( )
;.其中正确的是( )
A.①②③④B.①②③C.①②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
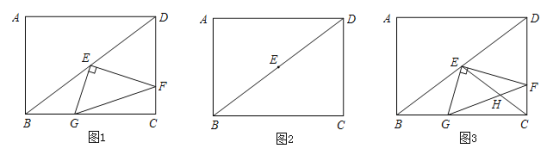
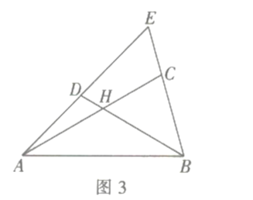
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是对角线BD的中点,直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G.
(1)若点F是边CD的中点,求EG的长.
(2)当直角∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC交于点F、G.∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值.
(3)当直角∠GEF绕顶点E旋转,旋转过程中与边CD、BC所在的直线交于点F、G.在图2中画出图形,并判断∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请直接写出tan∠EFG的值.
(4)如图3,连接CE交FG于点H,若![]() ,请求出CF的长.
,请求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
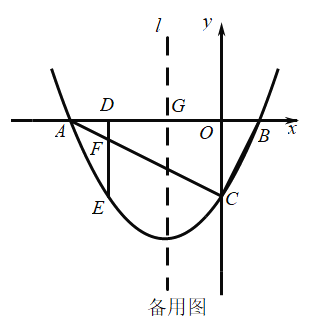
【题目】如图,抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标和抛物线的函数关系式;
的坐标和抛物线的函数关系式;
(2)点![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,在(2)的条件下,点
,在(2)的条件下,点![]() 是抛物线对称轴上一点,点
是抛物线对称轴上一点,点![]() 是坐标平面内一点,是否存在点
是坐标平面内一点,是否存在点![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请求出点
为顶点的四边形是菱形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
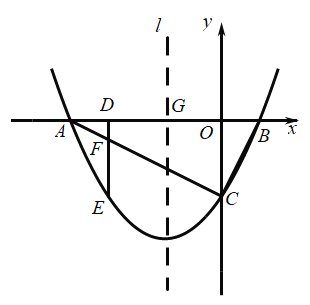
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
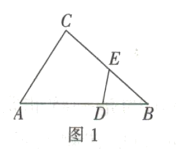
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
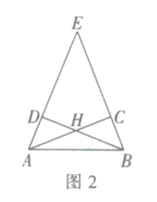
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,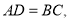 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com