
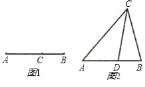
【题目】如图1所示,点C将线段AB分成两部分,如果![]() ,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图2所示,则直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
(2)请你说明:三角形的中线是否是该三角形的黄金分割线.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
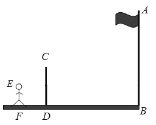
【题目】如图,九(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,PA、PB是⊙O的切线,切点分别为A、B,AC是⊙O的直径.
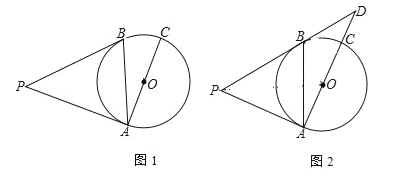
(1)如图1,若∠BAC=25°,求∠P的度数;
(2)如图2,延长PB、AC相交于点D.若AP=AC,求cosD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
(1)求△ACD的面积(用含a的代数式表示);
(2)求点D到射线BN的距离(用含有a的代数式表示);
(3)是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣(x﹣1)2+m(m是常数),点A(x1,y1),B(x2,y2)在抛物线上,若x1<1<x2,x1+x2>2,则下列大小比较正确的是( )
A. m>y1>y2 B. m>y2>y1 C. y1>y2>m D. y2>y1>m
查看答案和解析>>
科目:初中数学 来源: 题型:
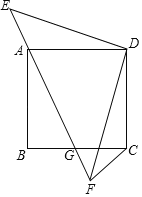
【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直角梯形OABC中,CB∥OA,对角线OB和AC交于点D,OC=2,CB=2,OA=4,点P为对角线CA上的一点,过点P作QH⊥OA于H,交CB的延长线于点Q,连接BP,如果△BPQ和△PHA相似,则点P的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com