
【题目】已知,PA、PB是⊙O的切线,切点分别为A、B,AC是⊙O的直径.
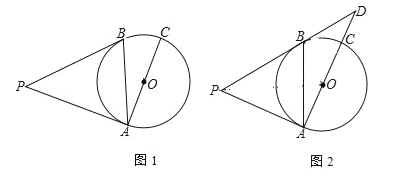
(1)如图1,若∠BAC=25°,求∠P的度数;
(2)如图2,延长PB、AC相交于点D.若AP=AC,求cosD的值.
【答案】(1)50°;(2)cosD=![]() .
.
【解析】
(1)连接OB.根据平行的想得到PA⊥AO,PB⊥OB,根据四边形的内角和即可得到结论;
(2)连结OP交AB于点E,再连OB、BC,根据切线的性质得到∠PAC=∠PBO=90°,推出OP是AB的垂直平分线,根据相似三角形的性质即可得到结论.
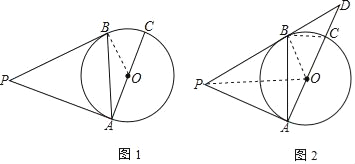
(1)证明:如图1,连接OB.
∵PA、PB分别切⊙O于A、B两点,
∴PA⊥AO,PB⊥OB,
∴∠PAO=∠PBO=90°.
∵∠BAC=25°,OB=OA,
∴∠BOA=180°﹣25°﹣25°=130°,
∴∠P=360°﹣90°﹣90°﹣130°=50°;
(2)解:如图2,连结OP交AB于点E,再连OB、BC,
∵PA、PB是⊙O的切线,
∴∠PAC=∠PBO=90°,
∵AP=AC,AC是⊙O的直径,
∴![]() ,∵PB=PA,OB=OA,
,∵PB=PA,OB=OA,
∴OP是AB的垂直平分线,
∵∠OAP=90°,AE⊥OP,
∴△OEA∽△AEP∽△OAP,
∴![]() ,
,
设OE=a,可得AE=BE=BC=2a,PE=4a,
∴OP=5a,
∴OA=![]() a,PA=PB=2
a,PA=PB=2![]() a,
a,
∵∠ABC=∠AEO=90°,
∴OP∥BC,
∴△DBC∽△DPO,
∴![]() =
=![]() =
=![]() =
=![]() .
.
∴BD=![]() ,OD=
,OD=![]()
![]() a,
a,
∴COSD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
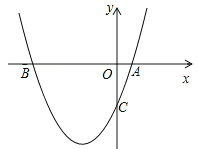
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60度的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
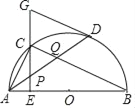
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
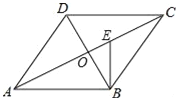
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求线段OE的长.
,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
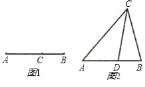
【题目】如图1所示,点C将线段AB分成两部分,如果![]() ,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点,如图2所示,则直线CD是△ABC的黄金分割线,你认为对吗?说说你的理由;
(2)请你说明:三角形的中线是否是该三角形的黄金分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
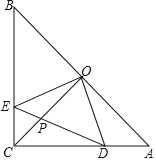
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论
(1) △AOD≌△COE;(2) OE=OD;(3) △EOP∽△CDP.
其中正确的结论是( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com