练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，

    （1）若∠BDO=∠CEO，求证：BE=CD．

    （2）若点E为AC中点，问点D满足什么条件时候，．

    【答案】（1）详见解析；（2）详见解析.

    【解析】分析：

    （1）由AB=AC可得∠ABC=∠ACB，结合∠BDO=∠CEO和BC=CB可得△DBC≌△ECB，由此可得BE=CD；

    （2）由E为AC中点可知，若此时D为AB的中点，则由三角形中位线定理可得DE∥BC，DE=BC，从而可得△DEO∽△BCO，由此即可得到.

    详解：

    （1）∵AB=AC，

    ∴∠ABC=∠ACB，

    在△DBC与△ECB中， ，

    ∴△DBC≌△ECB，

    ∴BE=CD；

    （2）当点D为AB的中点时，，理由如下：
    ∵点E为AC中点，点D为AB的中点，

    ∴DE=BC，DE∥BC，

    ∴△DEO∽△BCO，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，矩形ABCD中，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O.

    (1)如图1，连接AF、CE，求证:四边形AFCE为菱形；

    (2)如图2，若AB=4cm，AF=5cm，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止，在运动过程中：

    ①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求的值；

    ②若点P、Q的运动路程分别为(单位:cm，)，已知A、C、P、Q四点为顶点的四边形是平行四边形，求与满足的数量关系式。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若干名工人某天生产同一种玩具，生产的玩具数整理成条形图(如图所示)．则他们生产的玩具数的平均数、中位数、众数分别为（ ）

    A．5，5，4 B．5，5，5

    C．5，4，5 D．5，4，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）阅读下面材料：

    点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为|AB|．

    当A，B两点中有一点在原点时，不妨设点A在原点，如图（1），|AB|=|OB|=|b|=|a﹣b|；当A，B两点都不在原点时，

    ①如图（2），点A，B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；

    ②如图（3），点A，B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；

    ③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=|a﹣b|；

    综上，数轴上A，B两点之间的距离|AB|=|a﹣b|．

    （2）回答下列问题：

    ①数轴上表示2和5的两点之间的距离是　　，数轴上表示﹣2和﹣5的两点之间的距离是　　，数轴上表示1和﹣3的两点之间的距离是　　；

    ②数轴上表示x和﹣1的两点A和B之间的距离是　　，如果|AB|=2，那么x为　　；

    ③当代数式|x+1|+|x﹣2|取最小值时，相应的x的取值范围是　　．

    ④解方程|x+1|+|x﹣2|=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在菱形ABCD中，AC是对角线.

    (1)如图①,若AB=6,则菱形ABCD的周长为______；若∠DAB=70，则∠D的度数是_____；∠DCA的度数是____；

    (2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】东东在研究数学问题时遇到一个定义：将三个已经排好顺序数：x1，x2，x3，称为数列x1，x2，x3．计算|x1|，，，将这三个数的最小值称为数列x1，x2，x3的最佳值．例如，对于数列2，-1，3，因为|2|=2，=，=，所以数列2，-1，3的最佳值为．

    东东进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值．如数列-1，2，3的最佳值为；数列3，-1，2的最佳值为1；…．经过研究，东东发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为．根据以上材料，回答下列问题：

    （1）数列-4，-3，1的最佳值为

    （2）将“-4，-3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为 ，取得最佳值最小值的数列为 （写出一个即可）；

    （3）将2，-9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的最佳值为1，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，第一象限内的点A、B在反比例函数的图象上，点C在y轴上，BC∥x轴，点A的坐标为（2，4），且tan∠ACB=

    求：（1）反比例函数的解析式；

    （2）点C的坐标；

    （3）sin∠ABC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知A（，y1），B（2，y2）为反比例函数y=图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）

    A.（，0） B.（1，0） C.（，0） D.（，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

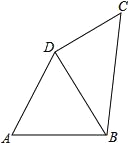
    【题目】如图，在四边形ABCD中，AB=AD=8，∠A=60°，∠ADC=150°，四边形ABCD的周长为32．

    （1）求∠BDC的度数；

    （2）四边形ABCD的面积．

    查看答案和解析>>

    同步练习册答案