
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌABЁЮCDЃЌЁЯB=90ЁуЃЌAB=AD=5ЃЌBC=4ЃЌMЁЂNЁЂEЗжБ№ЪЧABЁЂADЁЂCBЩЯЕФЕуЃЌAM=CE=1ЃЌAN=3ЃЌЕуPДгЕуMГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯпMBЉBEЯђЕуEдЫЖЏЃЌЭЌЪБЕуQДгЕуNГіЗЂЃЌвдЯрЭЌЕФЫйЖШбиелЯпNDЉDCЉCEЯђЕуEдЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяКѓЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЎЩшЁїAPQЕФУцЛ§ЮЊSЃЌдЫЖЏЪБМфЮЊtУыЃЌдђSгыtКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓЮЊЃЈ ЃЉ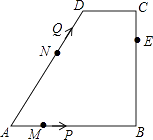
A.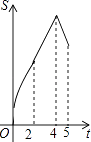
B.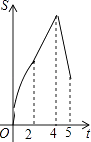
C.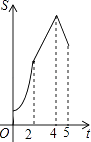
D.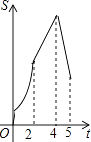
ЁОД№АИЁПD
ЁОНтЮіЁПНтЃКЁпAD=5ЃЌAN=3ЃЌ
ЁрDN=2ЃЌ
ШчЭМ1ЃЌЙ§ЕуDзїDFЁЭABЃЌ
ЁрDF=BC=4ЃЌ
дкRTЁїADFжаЃЌAD=5ЃЌDF=4ЃЌИљОнЙДЙЩЖЈРэЕУЃЌAF= ![]() =3ЃЌ
=3ЃЌ
ЁрBF=CD=2ЃЌЕБЕуQЕНЕуDЪБгУСЫ2sЃЌ
ЁрЕуPвВдЫЖЏ2sЃЌ
ЁрAP=3ЃЌМДQPЁЭABЃЌ
ЁржЛЗжШ§жжЧщПіЃК
ЂйЕБ0ЃМtЁм2ЪБЃЌШчЭМ1ЃЌ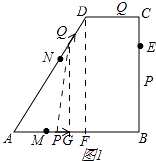
Й§QзїQGЁЭABЃЌЙ§ЕуDзїDFЁЭABЃЌQGЁЮDFЃЌ
Ёр ![]() ЃЌ
ЃЌ
гЩЬтвтЕУЃЌNQ=tЃЌMP=tЃЌ
ЁпAM=1ЃЌAN=3ЃЌ
ЁрAQ=t+3ЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁрQG= ![]() ЃЈt+3ЃЉЃЌ
ЃЈt+3ЃЉЃЌ
ЁпAP=t+1ЃЌ
ЁрS=SЁїAPQ= ![]() APЁСQG=
APЁСQG= ![]() ЁСЃЈt+1ЃЉЁС
ЁСЃЈt+1ЃЉЁС ![]() ЃЈt+3ЃЉ=
ЃЈt+3ЃЉ= ![]() ЃЈt+2ЃЉ2Љ
ЃЈt+2ЃЉ2Љ ![]() ЃЌ
ЃЌ
ЕБt=2ЪБЃЌS=6ЃЌ
ЂкЕБ2ЃМtЁм4ЪБЃЌШчЭМ2ЃЌ
ЁпAP=AM+t=1+tЃЌ
ЁрS=SЁїAPQ= ![]() APЁСBC=
APЁСBC= ![]() ЃЈ1+tЃЉЁС4=2ЃЈt+1ЃЉ=2t+2ЃЌ
ЃЈ1+tЃЉЁС4=2ЃЈt+1ЃЉ=2t+2ЃЌ
ЕБt=4ЪБЃЌS=8ЃЌ
ЂлЕБ4ЃМtЁм5ЪБЃЌШчЭМ3ЃЌ
гЩЬтвтЕУCQ=tЉ4ЃЌPB=t+AMЉAB=t+1Љ5=tЉ4ЃЌ
ЁрPQ=BCЉCQЉPB=4ЉЃЈtЉ4ЃЉЉЃЈtЉ4ЃЉ=12Љ2tЃЌ
ЁрS=SЁїAPQ= ![]() PQЁСAB=
PQЁСAB= ![]() ЁСЃЈ12Љ2tЃЉЁС5=Љ5t+50ЃЌ
ЁСЃЈ12Љ2tЃЉЁС5=Љ5t+50ЃЌ
ЕБt=5ЪБЃЌS=5ЃЌ
ЁрSгыtЕФКЏЪ§ЙиЯЕЪНЗжБ№ЪЧЂйS=SЁїAPQ= ![]() ЃЈt+2ЃЉ2Љ
ЃЈt+2ЃЉ2Љ ![]() ЃЌЕБt=2ЪБЃЌS=6ЃЌЂкS=SЁїAPQ=2t+2ЃЌЕБt=4ЪБЃЌS=8ЃЌЂлЁрS=SЁїAPQ=Љ5t+50ЃЌЕБt=5ЪБЃЌS=5ЃЌ
ЃЌЕБt=2ЪБЃЌS=6ЃЌЂкS=SЁїAPQ=2t+2ЃЌЕБt=4ЪБЃЌS=8ЃЌЂлЁрS=SЁїAPQ=Љ5t+50ЃЌЕБt=5ЪБЃЌS=5ЃЌ
злКЯвдЩЯШ§жжЧщПіЃЌDе§ШЗ
ЙЪбЁDЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫШ§НЧаЮЕФУцЛ§КЭОиаЮЕФаджЪЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеШ§НЧаЮЕФУцЛ§=1/2ЁСЕзЁСИпЃЛОиаЮЕФЫФИіНЧЖМЪЧжБНЧЃЌОиаЮЕФЖдНЧЯпЯрЕШВХФме§ШЗНтД№ДЫЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌDЪЧBCЩЯШЮвтвЛЕуЃЌЙ§ЕуDЗжБ№ЯђABЁЂACв§ДЙЯпЃЌДЙзуЗжБ№ЮЊЕуEЁЂF.
(1)ШчЭМЂйЃЌЕБЕуDдкBCЕФЪВУДЮЛжУЪБЃЌDEЃНDFЃПВЂжЄУїЃЛ
(2)дкТњзуЕквЛЮЪЕФЬѕМўЯТЃЌСЌНгADЃЌДЫЪБЭМжаЙВгаМИЖдШЋЕШШ§НЧаЮЃПЧыаДГіЫљгаЕФШЋЕШШ§НЧаЮ(ВЛБижЄУї)ЃЛ
(3)ШчЭМЂкЃЌЙ§ЕуCзїABБпЩЯЕФИпCGЃЌЧыЮЪDEЁЂDFЁЂCGЕФГЄжЎМфДцдкдѕбљЕФЕШСПЙиЯЕЃПВЂМгвджЄУїЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љ ![]() гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЛЕуQЪЧвдCЃЈ0ЃЌЉ1ЃЉЮЊдВаФЁЂ1ЮЊАыОЖЕФдВЩЯвЛЖЏЕуЃЌЙ§QЕуЕФЧаЯпНЛЯпЖЮABгкЕуPЃЌдђЯпЖЮPQЕФзюаЁЪЧ ЃЎ
гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЛЕуQЪЧвдCЃЈ0ЃЌЉ1ЃЉЮЊдВаФЁЂ1ЮЊАыОЖЕФдВЩЯвЛЖЏЕуЃЌЙ§QЕуЕФЧаЯпНЛЯпЖЮABгкЕуPЃЌдђЯпЖЮPQЕФзюаЁЪЧ ЃЎ 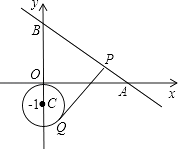
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=Љ ![]() [ЃЈxЉ2ЃЉ2+n]гыxжсНЛгкЕуAЃЈmЉ2ЃЌ0ЃЉКЭBЃЈ2m+3ЃЌ0ЃЉЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌСЌНсBCЃЎ
[ЃЈxЉ2ЃЉ2+n]гыxжсНЛгкЕуAЃЈmЉ2ЃЌ0ЃЉКЭBЃЈ2m+3ЃЌ0ЃЉЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌСЌНсBCЃЎ
ЃЈ1ЃЉЧѓmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуNЮЊХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЧвЮЛгкжБЯпBCЩЯЗНЃЌСЌНгCNЁЂBNЃЎЧѓЁїNBCУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуMЁЂPЗжБ№ЮЊЯпЖЮBCКЭЯпЖЮOBЩЯЕФЖЏЕуЃЌСЌНгPMЁЂPCЃЌЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЁїPCMЮЊЕШбќШ§НЧаЮЃЌЁїPMBЮЊжБНЧШ§НЧаЮЭЌЪБГЩСЂЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
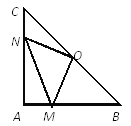
ЁОЬтФПЁПдкRtЁїABCжаЃЌABЃНACЃЌЁЯBAC=90ЁуЃЌOЮЊBCЕФжаЕуЁЃ
ЃЈ1ЃЉаДГіЕуOЕНЁїABCЕФШ§ИіЖЅЕуAЁЂBЁЂCЕФОрРыЕФДѓаЁЙиЯЕВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЙћЕуMЁЂNЗжБ№дкЯпЖЮABЁЂACЩЯвЦЖЏЃЌдквЦЖЏжаБЃГжANЃНBMЃЌЧыХаЖЯЁїOMNЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
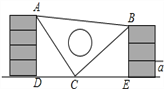
ЁОЬтФПЁППЮМфЃЌаЁУїФУзХРЯЪІЕФЕШбќШ§НЧАхЭцЃЌВЛаЁаФЕєЕНСНЧНжЎМфЃЌШчЭМЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADCЁеЁїCEBЃЛ
ЃЈ2ЃЉДгШ§НЧАхЕФПЬЖШПЩжЊAC=25cmЃЌЧыФуАяаЁУїЧѓГіЦіЧНзЉПщЕФКёЖШaЕФДѓаЁЃЈУППщзЉЕФКёЖШЯрЕШЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇЯАСЫЭМаЮЕФа§зЊжЊЪЖКѓЃЌЪ§бЇаЫШЄаЁзщЕФЭЌбЇУЧгжНјвЛВНЖдЭМаЮа§зЊЧАКѓЕФЯпЖЮжЎМфЁЂНЧжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎ 
ЃЈвЛЃЉГЂЪдЬНОП
ШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌAB=ADЃЌЁЯBAD=60ЁуЃЌЁЯABC=ЁЯADC=90ЁуЃЌЕуEЁЂFЗжБ№дкЯпЖЮBCЁЂCDЩЯЃЌЁЯEAF=30ЁуЃЌСЌНгEFЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌНЋЁїABEШЦЕуAФцЪБеыа§зЊ60ЁуКѓЕУЕНЁїAЁфBЁфEЁфЃЈAЁфBЁфгыADжиКЯЃЉЃЌЧыжБНгаДГіЁЯEЁфAF=ЖШЃЌЯпЖЮBEЁЂEFЁЂFDжЎМфЕФЪ§СПЙиЯЕЮЊ ЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌЕБЕуEЁЂFЗжБ№дкЯпЖЮBCЁЂCDЕФбгГЄЯпЩЯЪБЃЌЦфЫћЬѕМўВЛБфЃЌЧыЬНОПЯпЖЮBEЁЂEFЁЂFDжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌАб
ЃЌАб![]() ШЦзХ
ШЦзХ![]() ЕуФцЪБеыа§зЊЃЌЕУЕН
ЕуФцЪБеыа§зЊЃЌЕУЕН![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯ.
ЩЯ.
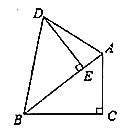
ЃЈ1ЃЉШє![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЖШЪ§ЃЛ
ЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() жа
жа![]() БпЩЯЕФИп.
БпЩЯЕФИп.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
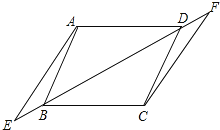
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуEЁЂFдкЫФБпаЮABCDЕФЖдНЧЯпBDЫљдкЕФжБЯпЩЯЃЌЧвBE=DFЃЌAEЁЮCFЃЌЧыдйЬэМгвЛИіЬѕМўЃЈВЛвЊдкЭМжадйдіМгЦфЫќЯпЖЮКЭзжФИЃЉЃЌФмжЄУїЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌВЂжЄУїФуЕФЯыЗЈ.
ФуЫљЬэМгЕФЬѕМўЃК____________________________________ЃЛ
жЄУїЃК
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com