
【题目】如图,![]() 中,
中,![]() ,把
,把![]() 绕着
绕着![]() 点逆时针旋转,得到
点逆时针旋转,得到![]() ,点
,点![]() 在
在![]() 上.
上.
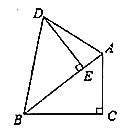
(1)若![]() ,求得
,求得![]() 度数;
度数;
(2)若![]() ,
,![]() ,求
,求![]() 中
中![]() 边上的高.
边上的高.
【答案】(1)∠BAC =50°;(2)![]()
【解析】
解:(1) 由旋转得△ACB≌△DEB
∴BD = BA
∴∠BAD =∠BDA=![]()
∴∠ABD=![]()
∴∠ABC =∠ABD=![]()
∵∠C=![]()
∴∠BAC=![]() ·········································································· 5分
·········································································· 5分
(2) ∵BC = 8,AC= 6,∠C=![]()
∴![]()
∵∠DEB =∠C=![]() 且BE=BC= 8,DE ="AC" = 6
且BE=BC= 8,DE ="AC" = 6
∴AE =" AB" – BE = 2
在Rt△DEA中,![]()
设AD边上的高为h
∴![]()
∴![]() ······················································· 10分
······················································· 10分


科目:初中数学 来源: 题型:
【题目】根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图: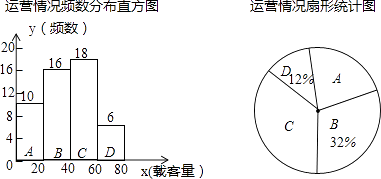
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )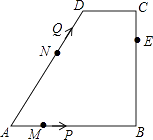
A.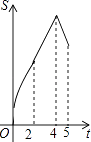
B.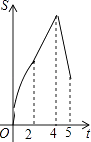
C.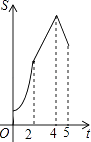
D.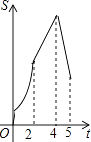
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( ) 
A.( ![]() )6
)6
B.( ![]() )7
)7
C.( ![]() )6
)6
D.( ![]() )7
)7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过(2,3)和(﹣1,﹣3),直线l2经过原点O,且与直线l1交于点P(﹣2,a).
(1)求a的值;
(2)(﹣2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点A,你能求出△APO的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
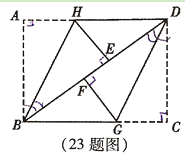
【题目】(10分) 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
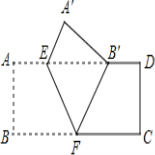
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
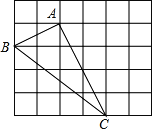
【题目】如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解决下列问题:
(1)通过计算判断△ABC的形状;
(2)在图中确定一个格点D,连接AD、CD,使四边形ABCD为平行四边形,并求出 □ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G. 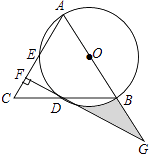
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com