
����Ŀ����ͼ1��������y=�� ![]() [��x��2��2+n]��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
[��x��2��2+n]��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��1����m��n��ֵ��
��2����ͼ2����NΪ�������ϵ�һ���㣬��λ��ֱ��BC�Ϸ�������CN��BN�����NBC��������ֵ��
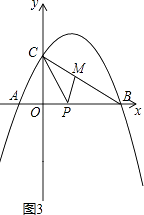
��3����ͼ3����M��P�ֱ�Ϊ�߶�BC���߶�OB�ϵĶ��㣬����PM��PC���Ƿ���������ĵ�P��ʹ��PCMΪ���������Σ���PMBΪֱ��������ͬʱ�����������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������ߵĽ���ʽΪy=�� ![]() [��x��2��2+n]=��
[��x��2��2+n]=�� ![]() ��x��2��2��
��x��2��2�� ![]() n��
n��
�������ߵĶԳ���Ϊֱ��x=2��
�ߵ�A�͵�BΪ�ԳƵ㣬
��2����m��2��=2m+3��2�����m=1��
��A����1��0����B��5��0����
��A����1��0������y=�� ![]() [��x��2��2+n]��9+n=0�����n=��9
[��x��2��2+n]��9+n=0�����n=��9
��2��
�⣺��ND��y�ύBC��D����ͼ2��
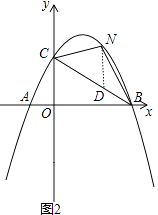
�����߽���ʽΪy=�� ![]() [��x��2��2��9]=��
[��x��2��2��9]=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��x=0ʱ��y=3����C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��5��0����C��0��3������� ![]() �����
����� 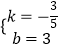 ��
��
��ֱ��BC�Ľ���ʽΪy=�� ![]() x+3��
x+3��
��N��x���� ![]() x2+
x2+ ![]() x+3������D��x����
x+3������D��x���� ![]() x+3����
x+3����
��ND=�� ![]() x2+
x2+ ![]() x+3������
x+3������ ![]() x+3��=��
x+3��=�� ![]() x2+3x��
x2+3x��
��S��NBC=S��NDC+S��NDB= ![]() 5ND=��
5ND=�� ![]() x2+
x2+ ![]() x=����x��
x=����x�� ![]() ��2+
��2+ ![]() ��
��
��x= ![]() ʱ����NBC���������ֵΪ
ʱ����NBC���������ֵΪ ![]()
��3��
��B��5��0����C��0��3����
��BC= ![]() =
= ![]() ��
��
����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC��
��PM=t����CM=t��MB= ![]() ��t��
��t��
�ߡ�MBP=��OBC��
���BMP�ס�BOC��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() �����t=
�����t= ![]() ��BP=
��BP= ![]() ��
��
��OP=OB��BP=5�� ![]() =
= ![]() ��
��
��ʱP������Ϊ�� ![]() ��0����
��0����
����MPB=90�㣬��MP=MC��
��PM=t����CM=t��MB= ![]() ��t��
��t��
�ߡ�MBP=��CBO��
���BMP�ס�BCO��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() �����t=
�����t= ![]() ��BP=
��BP= ![]() ��
��
��OP=OB��BP=5�� ![]() =
= ![]() ��
��
��ʱP������Ϊ�� ![]() ��0����
��0����
����������P�������� ![]() ��0����
��0���� ![]() ��0����
��0����
����������1�����������ߵĽ���ʽȷ���Գ���Ϊֱ��x=2�������öԳ��Եõ�2����m��2��=2m+3��2���ⷽ�̿ɵ�m��ֵ���Ӷ��õ�A����1��0����B��5��0����Ȼ���A���������y=�� ![]() [��x��2��2+n]�����n��ֵ����2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��
[��x��2��2+n]�����n��ֵ����2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=�� ![]() x+3����N��x����
x+3����N��x���� ![]() x2+
x2+ ![]() x+3������D��x����
x+3������D��x���� ![]() x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=��
x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=�� ![]() x2+
x2+ ![]() x��Ȼ�����ö��κ�����������⣻��3�������ù��ɶ��������BC=
x��Ȼ�����ö��κ�����������⣻��3�������ù��ɶ��������BC= ![]() ���ٷ������ۣ�����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=
���ٷ������ۣ�����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB= ![]() ��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB=
��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB= ![]() ��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ������������ʽ������������ͼ�ε����ʣ��������������ε��ж������������Ʊȼ����߶εij����ʾ�߶�֮��Ĺ�ϵ��ѧ�����÷������۵�˼������ѧ���⣮
��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ������������ʽ������������ͼ�ε����ʣ��������������ε��ж������������Ʊȼ����߶εij����ʾ�߶�֮��Ĺ�ϵ��ѧ�����÷������۵�˼������ѧ���⣮
�����㾫����������Ҫ�����˶��κ��������ʺͱ����߶ε����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����ѡ��ͬһ���ȵ�λ���������߶�a��b�ij��ȷֱ�Ϊm��n����ô��˵�������߶εı���a/b=m/n����д��a��b=m��n������ȷ�����⣮


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+2x��6��x�ύ�ڵ�A����6��0����B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��BD�������߽��ڵ�D����D���C���ڸ������ߵĶԳ���Գƣ�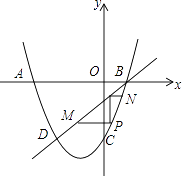
��1������CD���������ߵı���ʽ���߶�CD�ij��ȣ�
��2�����߶�BD�·�������������һ��P������P��PM��x�ᣬPN��y�ᣬ�ֱ�BD�ڵ�M��N������MPN��������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���Ȩƽ����ʱ��ͳ���г��ø��������ֵ���������ʵ�����ݣ��Ѹ����Ƶ��������Ӧ����ֵ��Ȩ��������������֪ʶ����������ʵ�����⣮
Ϊ�˽�5·������������Ӫ�������������ͳ����ij��5·��������ÿ�����а�ε��ؿ����������ؿ����Ķ��ٷֳ�A��B��C��D���飬�õ�����ͳ��ͼ��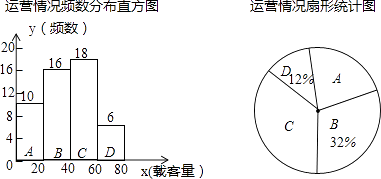
��1����A���Ӧ����Բ�ĽǵĶ�������д�������ؿ�������λ�����ڵ��飻
��2��������5·��������ƽ��ÿ����ؿ�����
��3�����һ���°�30����㣬�����5·��������һ���µ����ؿ��������ѽ���ÿ�ѧ��������ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ����a0=1����a2a3=a5����2��2=��![]() ��������3��5��+����2��4��8������1��=0����x2+x2=2x2��������ȷ���ǣ�������
��������3��5��+����2��4��8������1��=0����x2+x2=2x2��������ȷ���ǣ�������
A���٢ڢ�B���٢ۢ�
C���ڢۢ�D���ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ǡ����ܻ�������ɫ���С���ʶ����ǿ��Խ��Խ�����ϲ�������г����У�Ҳ�����г��̼Ҵ����̻���ij���г��о�Ӫ��A�����г�ȥ�������ܶ�Ϊ8��Ԫ������������г�ÿ���ۼ�Ԥ�Ʊ�ȥ�꽵��200Ԫ�������ͳ�������������ȥ����ͬ����ô����������ܶ��ȥ�����10%����
��1��A�����г�ȥ��ÿ���ۼ۶���Ԫ��
��2���ó��н���ƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ���������������֪��A�ͳ���B�ͳ��Ľ����۸�ֱ�Ϊ1500Ԫ��1800Ԫ���ƻ�B�ͳ����ۼ۸�Ϊ2400Ԫ��Ӧ�����֯��������ʹ�������г����ۻ�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABCD�У�EΪ�Խ���AC�ӳ����ϵ�һ�㣮
ABCD�У�EΪ�Խ���AC�ӳ����ϵ�һ�㣮
(1)���ı���ABCD�����Σ���֤��BE��DE.
(2)д��(1)�������⣬���ж�����������Ǽ����⣬���������⣬����֤�������Ǽ����⣬�ٳ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����B=90�㣬AB=AD=5��BC=4��M��N��E�ֱ���AB��AD��CB�ϵĵ㣬AM=CE=1��AN=3����P�ӵ�M��������ÿ��1����λ���ȵ��ٶ�������MB��BE���E�˶���ͬʱ��Q�ӵ�N����������ͬ���ٶ�������ND��DC��CE���E�˶���������һ���㵽�����һ����Ҳֹͣ�˶������APQ�����ΪS���˶�ʱ��Ϊt�룬��S��t������ϵ�Ĵ���ͼ��Ϊ�� ��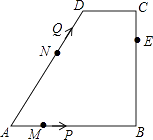
A.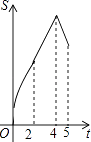
B.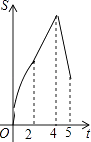
C.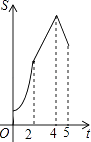
D.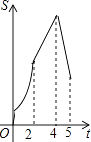
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����������ΪS1 �� ��CDΪб��������ֱ�������Σ��Ըõ���ֱ�������ε�һ��ֱ�DZ�Ϊ�������������Σ���������ΪS2 �� �������մ˹��ɼ�����ȥ����S9��ֵΪ�� �� 
A.�� ![]() ��6
��6
B.�� ![]() ��7
��7
C.�� ![]() ��6
��6
D.�� ![]() ��7
��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
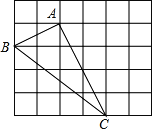
����Ŀ����ͼ�����ɱ߳�Ϊ1��С��������ɵ�5��6�������У���ABC������������ڸ���ϣ��밴Ҫ�����������⣺
��1��ͨ�������ж���ABC����״��
��2����ͼ��ȷ��һ�����D������AD��CD��ʹ�ı���ABCDΪƽ���ı��Σ������ ��ABCD�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com