Question

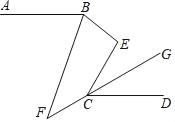
【题目】如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F=33°，则∠E=_____．

Answer 1

【答案】82°

【解析】

过F作FH∥AB，依据平行线的性质，可设∠ABF=∠EBF=α=∠BFH，∠DCG=∠ECG=β=∠CFH，根据四边形内角和以及∠E-∠F=33°，即可得到∠E的度数．

如图，过F作FH∥AB，

∵AB∥CD，

∴FH∥AB∥CD，

∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，

∴可设∠ABF=∠EBF=α=∠BFH，∠DCG=∠ECG=β=∠CFH，

∴∠ECF=180°﹣β，∠BFC=∠BFH﹣∠CFH=α﹣β，

∴四边形BFCE中，∠E+∠BFC=360°﹣α﹣（180°﹣β）=180°﹣（α﹣β）=180°﹣∠BFC，

即∠E+2∠BFC=180°，①

又∵∠E﹣∠BFC=33°，

∴∠BFC=∠E﹣33°，②

∴由①②可得，∠E+2（∠E﹣33°）=180°，

解得∠E=82°，

故答案是：82°．