
分析 首先根据题意作出图形,由多边形的内角和公式,得出内角,可得△OBC是等边三角形,然后由三角函数的性质,求得OH的长,继而求得正六边形的面积.
解答 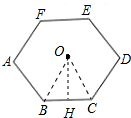 解:如图,连接OB,OC,过点O作OH⊥BC于H,
解:如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,
∴∠BOC=×360°=60°,
∵OB=0C,
∴△OBC是等边三角形,
∴BC=OB=OC=1,
∴内角为:$\frac{180×(6-2)}{6}$=120°;
∵在Rt△OBH中,OH=OB•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴S正六边形ABCDEF=6S△OBC=6×$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
故答案为:120,$\frac{3\sqrt{3}}{2}$.
点评 本题考查了正多边形和圆,以及圆的内接正六边形的性质、正多边形的内角和、等边三角形的判定与性质以及三角函数等知识.此题难度不大,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
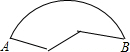 小明不慎把一个圆盘摔碎了,只剩下如图所示的一块比较完整的部分,他想找工人师傅做一个跟原来一样的圆盘,需要知道圆盘原来的形状,你能帮小明画出来吗?(用圆规、直尺作图,不写作法,但要保留作图痕迹.)
小明不慎把一个圆盘摔碎了,只剩下如图所示的一块比较完整的部分,他想找工人师傅做一个跟原来一样的圆盘,需要知道圆盘原来的形状,你能帮小明画出来吗?(用圆规、直尺作图,不写作法,但要保留作图痕迹.)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 与字母a,b都有关 | B. | 只与字母a有关 | C. | 只与字母b有关 | D. | 与字母a,b都无关 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
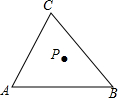 如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )| A. | ∠A,∠B的平分线的交点处 | |
| B. | AB的垂直平分线与∠B的平分线的交点处 | |
| C. | BC的垂直平分线与∠A的平分线的交点处 | |
| D. | AB,BC的垂直平分线的交点处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<2且m≠1 | B. | m>2 | C. | m<-2 | D. | m<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com