
【题目】已知,如图,矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作DEFG.
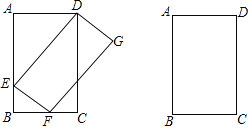
(1)求DEFG对角线DF的长;
(2)求DEFG周长的最小值;
(3)当DEFG为矩形时,连接BG,交EF,CD于点P,Q,求BP:QG的值.
【答案】(1)DF的长![]() ;(2)DEFG周长的最小值:
;(2)DEFG周长的最小值:![]() ;(3)BP:QG的值为
;(3)BP:QG的值为![]() 或
或![]() .
.
【解析】
(1)DEFG对角线DF的长就是Rt△DCF的斜边的长,由勾股定理求解;
(2)DEFG周长的最小值就是求邻边2(DE+EF)最小值,DE+EF的最小值就是以AB为对称轴,作点F的对称点M,连接DM交AB于点N,点E与N点重合时即DE+EF=DM时有最小值,在Rt△DMC中由勾股定理求DM的长;
(3)DEFG为矩形时有两种情况,一是一般矩形,二是正方形,分类用全等三角形判定与性质,等腰直角三角形判定与性质,三角形相似的判定与性质和勾股定理求解.
(1)如图1所示:
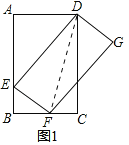
连接DF,
∵四边形ABCD是矩形,
∠C=90°,AD=BC,AB=DC,
∵BF=FC,AD=2;∴FC=1,
∵AB=3;∴DC=3,
在Rt△DCF中,由勾股定理得,
∴DF=![]() ;
;
故DEFG对角线DF的长![]() .
.
(2)如图2所示:
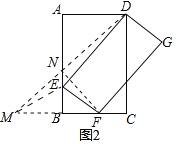
作点F关直线AB的对称点M,连接DM交AB于点N,
连接NF,ME,点E在AB上是一个动点,
①当点E不与点N重合时点M、E、D可构成一个三角形,
∴ME+DE>MD,
②当点E与点N重合时点M、E(N)、D在同一条直线上,
∴ME+DE=MD
由①和②DE+EF的值最小时就是点E与点N重合时,
∵MB=BF,∴MB=1,
∴MC=3,
又∵DC=3,
∴△MCD是等腰直角三角形,
∴MD=![]() ,
,
∴NF+DF=MD=2![]() ,
,
∴lDEFG=2(NF+DF)=4![]() ;
;
(3)①当AE=1,BE=2时,过点B作BH⊥EF,
如图3(甲)所示:
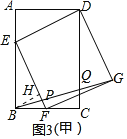
∵DEFG为矩形,
∴∠A=∠ABF=90°,
又∵BF=
∴在△ADE和△BEF中有,
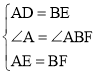 ,
,
∴△ADE≌△BEF中(SAS),
∴DE=EF,
∴矩形DEFG是正方形;
在Rt△EBF中,由勾股定理得:
EF=![]() ,
,
∴BH![]() ,
,
又∵△BEF~△FHB,
∴![]() ,
,
HF=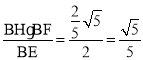 ,
,
在△BPH和△GPF中有:
![]() ,
,
∴△BPH∽△GPF(AA),
∴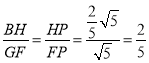
∴PF=![]() ,
,
又∵EP+PF=EF,
∴![]() ,
,
又∵AB∥BC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
∴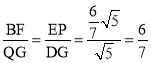 .
.
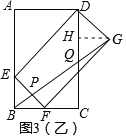
②当AE=2,BE=1时,过点G作GH⊥DC,
如图3(乙)所示:
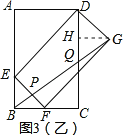
∵DEFG为矩形,
∴∠A=∠EBF=90°,
∵AD=AE=2,BE=BF=1,
∴在Rt△ADE和Rt△EFB中,由勾股定理得:
∴ED=![]() ,
,
EF=![]() ,
,
∴∠ADE=45°,
又∵四边形DEFG是矩形,
∴EF=DG,∠EDG=90°,
∴DG=![]() ,∠HDG=45°,
,∠HDG=45°,
∴△DHG是等腰直角三角形,
∴DH=HG=1,
在△HGQ和△BCQ中有,
![]()
∴△HGQ∽△BCQ(AA),
∴![]() ,
,
∵HC=HQ+CQ=2,
∴HQ=![]() ,
,
又∵DQ=DH+HQ,
∴DQ=1+![]() =
=![]() ,
,
∵AB∥DC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
∴![]() ,
,
综合所述,BP:QG的值为![]() 或
或![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
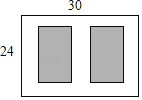
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
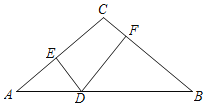
【题目】如图,在等腰三角形ACB中,AC=BC=10,AB=16,D为底边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为点E,F,则DE+DF等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解我市居民的低碳生活状况,适宜采用抽样调查的方法
B. 一组数据2,2,3,6的众数和中位数都是2
C. “掷一枚硬币正面朝上的概率是![]() ”,表示每抛硬币2次就有1次正面朝上
”,表示每抛硬币2次就有1次正面朝上
D. 随机抽取甲乙两名同学的5次数学成绩,平均分都是90分,方差分别是S甲2=5,S乙2=10,说明乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学从《中国好声音》、《歌手》、《蒙面唱将猜猜猜》三个综艺节目中都随机选择一个节目观看.
(1)甲同学观看《蒙面唱将猜猜猜》的概率是 ;
(2)求甲、乙两名同学观看同一节目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
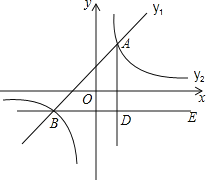
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | |||||
尺寸(cm) | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 | a | 9.03 | 9.04 | 9.06 | 9.07 | 9.08 | b |
按照生产标准,产品等次规定如下:
尺寸(单位:cm) | 产品等次 |
8.97≤x≤9.03 | 特等品 |
8.95≤x≤9.05 | 优等品 |
8.90≤x≤9.10 | 合格品 |
x<8.90或x>9.10 | 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种商品销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.求甲种商品与乙种商品的销售单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com