
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
【答案】(1)A的坐标为(2,0)、B的坐标为(0,2);(2)C的坐标为(![]() );(3)证明过程见解析.
);(3)证明过程见解析.
【解析】
(1)在直线![]() 中分别令y=0,x=0可求得A、B两点的坐标;
中分别令y=0,x=0可求得A、B两点的坐标;
(2)根据面积比,可以求得C的横纵坐标比,由C在直线AB上,代入直线解析式即可得出答案;
(3)根据条件可证△DBO≌△FOA,可得BD=FO,从而可得到BD+BF=BO,可得出结论.
解:(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点
两点
∴当x=0时,y=2;当y=0时,x=2
∴A的坐标为(2,0)、B的坐标为(0,2).
(2)∵![]()
∴![]()
又C在直线![]() 上
上
∴C的坐标为(![]() ).
).
(3)∵BD∥OA,AE⊥OC
∴∠D=∠DOA
∵∠DOA+∠DOF=90°
∠AFO+∠DOF=90°
∴∠DOA=∠AFO
∴∠D=∠AFO
在△DBO和△FOA中
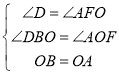
∴△DBO≌△FOA(AAS)
∴BD=FO
∴BD+BF=FO+BF=BO
∵BO=2
∴BD+BF=2
即BD+BF是定值不变.


科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫:平均每天可售出20件,每件盈利40元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经市场调查发现:如果每件衬衫降价1元,那么平均每天就可多售出2件.若商场想平均每天盈利达1200元,那么每件衬衫应降价多少元?你若是商场经理,为获得最大利润,每件衬衫应降价多少元,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
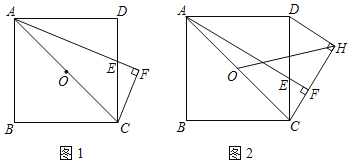
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
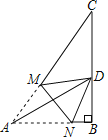
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() ,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为_____.
,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
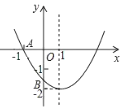
【题目】已知二次函数![]() (
(![]() )的图象与x轴交于点A(
)的图象与x轴交于点A(![]() ,0),与y轴的交点B在(0,
,0),与y轴的交点B在(0,![]() )和(0,
)和(0,![]() )之间(不包括这两点),对称轴为直线x=1.下列结论:①
)之间(不包括这两点),对称轴为直线x=1.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确个数结论有______.
.其中正确个数结论有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片片它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q)
(1)请用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数根的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点A的坐标为(﹣4,0),B的坐标为(1,0),且OC=4OB.
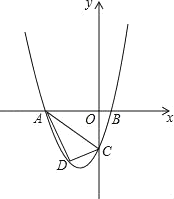
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求三角形ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com