
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
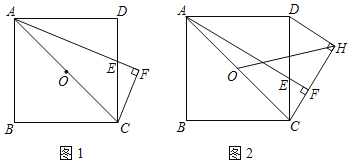
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
【答案】(1)证明见解析;(2)AF=![]() OH,理由见解析;(3)
OH,理由见解析;(3)![]() .
.
【解析】
(1)如图1,延长AD、CH交于M,证明△ACF≌△AMF(ASA),得CM=2CF,再证明△ADE≌△CDM(ASA),可得结论;
(2)如图2,作辅助线,构建全等三角形,证明△OMC≌△OND(AAS),并证明四边形MONH是正方形,得OH=![]() OM,根据三角形中位线定理可得是结论;
OM,根据三角形中位线定理可得是结论;
(3)如图1,证明△ADE∽△CFE,得CF=2EF,利用正方形的性质和勾股定理计算AD=CD=2,分别计算AE和EF的长可得结论.
(1)证明:如图1,延长AD、CH交于M,

∵AF⊥CF,
∴∠AFC=∠AFM=90°,
∵∠DAE=∠CAE,AF=AF,
∴△ACF≌△AMF(ASA),
∴CF=FM,
∴CM=2CF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADC=∠CDM=90°,
∵∠ADE=∠EFC=90°,∠AED=∠CEF,
∴∠ECF=∠EAD,
∴△ADE≌△CDM(ASA),
∴AE=CM=2CF;
(2)解:AF=![]() OH,理由是:
OH,理由是:
如图2,过O作ON⊥DH于N,OM⊥CH于M,连接OD,

∴∠OMH=∠ONH=∠MHN=90°,
∴四边形MONH为矩形,
∴∠MON=90°,
∵四边形ABCD是正方形,
∴OD=OC,∠DOC=90°,
∴∠MOC=∠DON,
∵∠OMC=∠OND=90°,
∴△OMC≌△OND(AAS),
∴OM=ON,
∴矩形MONH是正方形,
∴OH=![]() OM,
OM,
△ACF中,∵OA=OC,OM∥AF,
∴CM=FM,
∴AF=2OM,
∴![]() =
=![]() ,即AF=
,即AF=![]() OH;
OH;
(3)∵∠ADE=∠EFC=90°,∠AED=∠CEF,
∴△ADE∽△CFE,
∴![]() =
=![]() =
=![]() =2,
=2,
∵四边形ABCD是正方形,且AC=2![]() ,
,
∴AD=CD=2,
∵E是CD的中点,
∴DE=CE=1,
由勾股定理得:AE=![]() =
=![]() =
=![]() ,
,
设EF=x,则CF=2x,
∴CE=![]() x=1,
x=1,
x=![]() ,
,
∴EF=![]() ,
,
∴AF=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
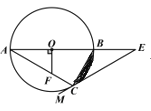
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司2月份销售新上市一种新型低能耗汽车20辆,由于该型汽车的优越的经济适用性,销量快速上升,4月份该公司销售该型汽车达到45辆,并且2月到3月和3月到4月两次的增长率相同.
(1)求该公司销售该型汽车每次的增长率;
(2)若该型汽车每辆的盈利为2万元,则平均每天可售10辆,为了尽量减少库存,汽车销售公司决定采取适当的降价措施,经调查发现,每辆汽车每降5000元,公司平均每天可多售出2辆,若汽车销售公司每天要获利14万元,每辆车需降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
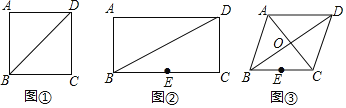
![]() 请在图
请在图![]() 的正方形ABCD的对角线BD上作一点P,使
的正方形ABCD的对角线BD上作一点P,使![]() 最小;
最小;
![]() 如图
如图![]() ,点P为矩形ABCD的对角线BD上一动点,
,点P为矩形ABCD的对角线BD上一动点,![]() ,
,![]() ,点E为BC边的中点,请作一点P,使
,点E为BC边的中点,请作一点P,使![]() 最小,并求这个最小值;
最小,并求这个最小值;
问题解决
![]() 如图
如图![]() ,李师傅有一块边长为1000米的菱形采摘园ABCD,
,李师傅有一块边长为1000米的菱形采摘园ABCD,![]() 米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离;若不存在,请说明理由.
米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)平移△ABC,若点A的对应点A1的坐标为(0,﹣4),画出平移后对应的△A1B1C1,并写出B1,C1的坐标;
(2)将△ABC以点C为旋转中心逆时针旋转90°,画出旋转后对应的△A2B2C2,并写出B2,C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com