
【题目】已知,如图抛物线y=ax2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点A的坐标为(﹣4,0),B的坐标为(1,0),且OC=4OB.
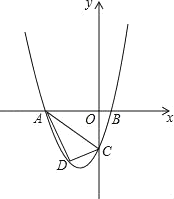
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求三角形ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
【答案】(1)y=x2+3x﹣4;(2)三角形ACD面积的最大值=8;(3)存在3个点符合题意,坐标分别是P1(﹣3,﹣4),P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).
【解析】
(1)根据点B的坐标为(1,0),OC=4OB可得出C点坐标,再把A,B,C三点的坐标代入抛物线的解析式求出a,b,c的值即可;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M,N,利用待定系数法求出直线AC的解析式,故可得出DM=(x+2)2+4,即可得出结论;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,根据PC两点的纵坐标相等可得出P点坐标;②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,令P(x,4),由x2+3x4=4得出x的值即可得出P点坐标.
解:(1)∵OC=4OB,B(1,0),
∴C(0,﹣4),
把点A,B,C的坐标代入y=ax2+bx+c,得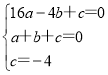
解得: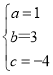 ,
,
∴抛物线线的解析式为:y=x2+3x﹣4;
(2)如图1,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
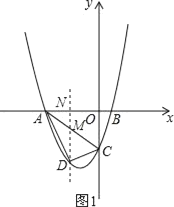
∵A(﹣4,0),B的坐标为(1,0),
∴AB=5,
∴S△ACD=![]() DM×(AN+ON)=
DM×(AN+ON)=![]() DMOA=2DM,
DMOA=2DM,
设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣4,0),C(0,﹣4),
∴![]() ,解得
,解得![]() ,
,
故直线AC的解析式为:y=﹣x﹣4.
令D(x,x2+3x﹣4),M(x,﹣x﹣4),则DM=﹣x﹣4﹣(x2+3x﹣4)=﹣(x+2)2+4,
当x=﹣2时,DM有最大值4,
故三角形ACD面积的最大值=![]() ×4×4=8;
×4×4=8;
(3)①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.
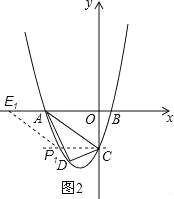
∵C(0,﹣4),令x2+3x﹣4=﹣4,
∴x=0或x=﹣3.
∴P1(﹣3,﹣4).
②如图3,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
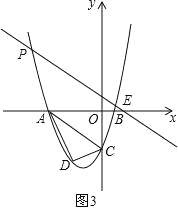
∵C(0,﹣4),
∴可令P(x,4),由x2+3x﹣4=4,得x2+3x﹣8=0.
解得x=![]() 或x=
或x=![]() .
.
此时存在点P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).
综上所述,存在3个点符合题意,坐标分别是P1(﹣3,﹣4),P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-(a+b)x2-2cx+a-b,a、b、c是△ABC的三边
(1) 当抛物线与x轴只有一个交点时,判断△ABC是什么形状
(2) 当![]() 时,该函数有最大值
时,该函数有最大值![]() ,判断△ABC是什么形状
,判断△ABC是什么形状
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)平移△ABC,若点A的对应点A1的坐标为(0,﹣4),画出平移后对应的△A1B1C1,并写出B1,C1的坐标;
(2)将△ABC以点C为旋转中心逆时针旋转90°,画出旋转后对应的△A2B2C2,并写出B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
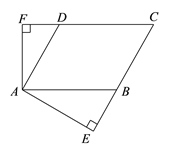
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
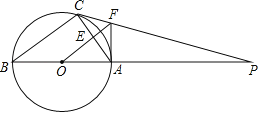
【题目】如图,![]() 内接于
内接于![]() ,AB是直径,
,AB是直径,![]() 的切线PC交BA的延长线于点P,
的切线PC交BA的延长线于点P,![]() 交AC于点E,交PC于点F,连接AF;
交AC于点E,交PC于点F,连接AF;
![]() 判断AF与
判断AF与![]() 的位置关系并说明理由.
的位置关系并说明理由.
![]() 若
若![]() 的半径为8,
的半径为8,![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
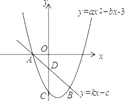
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com