
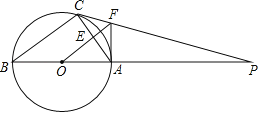
【题目】如图,![]() 内接于
内接于![]() ,AB是直径,
,AB是直径,![]() 的切线PC交BA的延长线于点P,
的切线PC交BA的延长线于点P,![]() 交AC于点E,交PC于点F,连接AF;
交AC于点E,交PC于点F,连接AF;
![]() 判断AF与
判断AF与![]() 的位置关系并说明理由.
的位置关系并说明理由.
![]() 若
若![]() 的半径为8,
的半径为8,![]() ,求AC的长.
,求AC的长.
【答案】(1)![]() 为圆O的切线,理由见解析;(2)
为圆O的切线,理由见解析;(2)![]() .
.
【解析】
(1)AF为为圆O的切线,理由为:连接OC,由PC为圆O的切线,利用切线的性质得到CP垂直于OC,由OF与BC平行,利用两直线平行内错角相等,同位角相等,分别得到两对角相等,根据OB=OC,利用等边对等角得到一对角相等,等量代换得到一对角相等,再由OC=OA,OF为公共边,利用SAS得出三角形AOF与三角形COF全等,由全等三角形的对应角相等及垂直定义得到AF垂直于OA,即可得证;
(2)根据平行线的性质可知:OE垂直于AC,利用面积法求出AE的长,即可确定出AC的长.
![]() 为圆O的切线,理由是:
为圆O的切线,理由是:
连接OC,

![]() 为圆O切线,
为圆O切线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,OA为
,OA为![]() 的半径,
的半径,
则AF为![]() 的切线;
的切线;
![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
则![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
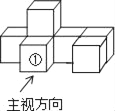
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
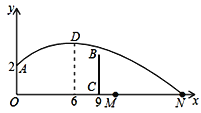
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个不透明的口袋中装有5个只有颜色不同的球,其中2个白球,3个黑球![]() 第一次随机摸出一个球,不放回,再随机摸出一个球.
第一次随机摸出一个球,不放回,再随机摸出一个球.
![]() Ⅰ
Ⅰ![]() 求第一次摸到黑球的概率;
求第一次摸到黑球的概率;
![]() Ⅱ
Ⅱ![]() 请用列表或画树状图等方法求两次都摸到黑球的概率.
请用列表或画树状图等方法求两次都摸到黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2+2mx+m﹣3=0总有实数根.
(1)求m的取值范围;
(2)在(1)的条件下,当m在取值范围内取最小整数时,求原方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)旋转角的大小;
(2)若AB=10,AC=8,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
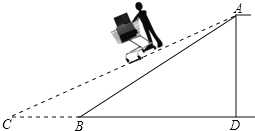
【题目】某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1:1.8改为1:2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
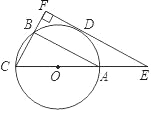
【题目】如图,△ABC内接于⊙O,AC是⊙O直径,D是![]() 的中点,过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点,过点D作CB的垂线,分别交CB、CA延长线于点F、E.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若sinE=![]() ,求AB:EF的值.
,求AB:EF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com