
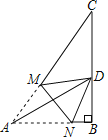
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() ,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为_____.
,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为_____.
【答案】![]() 或4
或4![]() ﹣6.
﹣6.
【解析】
△DCM为直角三角形,需要分两种情况进行讨论:当∠CDM=90°时;当∠CMD=90°时,分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到AN的长.
解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() ,
,
∴∠C=30°,AB=![]() AC=
AC=![]() ,
,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=![]() DN=
DN=![]() AN,
AN,
∴BN=![]() AB=
AB=![]() ,
,
∴AN=2BN=![]() ;
;
②如图,当∠CMD=90°时,△CDM是直角三角形,
由题意可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=![]() DN=
DN=![]() AN,BN=
AN,BN=![]() BD,
BD,
又∵AB=![]() ,
,
∴2BD+![]() BD=
BD=![]() ,
,
解得:BD=2![]() ﹣3,
﹣3,
∴AN=2BD=4![]() ﹣6;
﹣6;
综上所述,AN的长![]() 或4
或4![]() ﹣6;
﹣6;
故答案为:![]() 或4
或4![]() ﹣6.
﹣6.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】为了满足学生的个性化需求,新课程改革已经势在必行,某校积极开展拓展性课程建设,大体分为学科、文体、德育、其他等四个框架进行拓展课程设计。为了了解学生喜欢的拓展课程类型,学校随机抽取了部分学生进行调查,调查后将数据绘制成扇形统计图和条形统计图(未绘制完整).

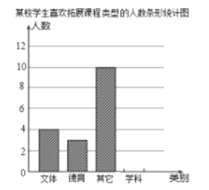
(1)求调查的学生总人数,并把条形图补充完整并填写扇形图中缺失的数据;
(2)小明同学说:“因为调查的同学中喜欢文体类拓展课程的同学占16%,而喜欢德育类拓展课程的同学仅占12%,所以全校2000名学生中,喜欢文体类拓展课程的同学人数一定比喜欢德育类拓展课程的同学人数多。”你觉得小明说得对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
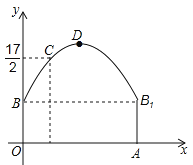
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
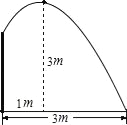
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
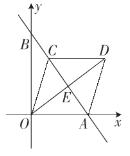
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )
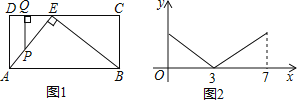
A. 2B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
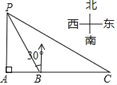
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.
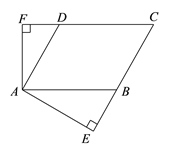
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com