练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：如图，D，E分别在△ABC的边BC，AC上，AD，BE交于点G，AD⊥BC，点F在AD上，且△EFG∽△BDG．
    求证：△AEF∽△ACD．
    考点：相似三角形的判定与性质
    专题：证明题
    分析：由△EFG∽△BDG可得∠FAE=∠DAC，可证△AEF∽△ACD．
    解答：证明：∵△EFG∽△BDG，
    ∴∠EFG=∠BDG=90°，
    ∴∠AFE=∠ADC=90°，
    ∵∠FAE=∠DAC，
    ∴△AEF∽△ACD．
    点评：本题考查了相似三角形的判定，考查了相似三角形对应角相等的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

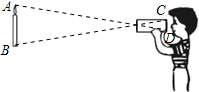    如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm，他准备了一支长为20cm的蜡烛，想要得到高度为4cm的像，蜡烛与纸筒的距离应该为（　　）
    A、60cmB、65cm
    C、70cmD、75cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列各数中，无理数是（　　）
    A、3.14
    B、
    22
    7
    C、
    π
    2
    D、
    		4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一元二次方程（x+1）2=9可转化为两个一元一次方程，其中一个一元一次方程是x+1=3，则另一个一元二次方程是（　　）
    A、x-1=-3
    B、x-1=3
    C、x+1=3
    D、x+1=-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在锐角△ABC中，AD是BC边上的高线，矩形EFGH的顶点E，H分别在AB，AC上，F，G在BC边上，AD与EH相交于点K．
    （1）如图1，若BC=10，AD=5，EH=2EF，求EF，EH的长．
    （2）如图2，若BC=AD=8，求矩形EFGH的周长．
    （3）如图3，若四边形EFGH是边长为4的正方形，且S△AEH：S△HGC：S△BEF=1：1：3，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

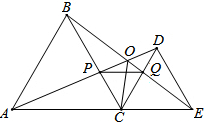    如图，△ABC、△CDE都是等边三角形，且点A、C、E在一条直线上，AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q．求证：
    （1）AD=BE，AP=BQ；
    （2）∠AOB=60°，OC平分∠AOE；
    （3）PQ∥AE；
    （4）△CPQ为等边三角形；
    （5）
    1
    PQ
    =
    1
    AC
    +
    1
    CE
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    什么是两点之间的距离？
     
    ；如果这两点是A、B，那么它们之间的距离指的是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AD⊥AB，AD=AB，CE=CD，BE⊥BD，试判断线段CD和线段CE的位置关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

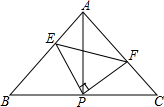    如图所示，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E，F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），给出以下五个结论：①AE=CF；②△EPF是等腰直角三角形；③S四边形AEPF=
    1
    2
    S△ABC；④EF=AP；⑤BE+CF=EF；上述结论中始终正确的有
     
    ．

    查看答案和解析>>

    同步练习册答案