
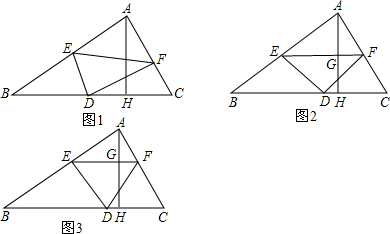
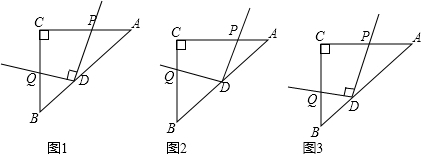
���� ��1���������������ε�����ȵ������Ʊȵ�ƽ�������DEF�������
��2����DP��EF��P����EF=x����EF��BC���õ��ɱ����߶Σ��������x��ֵ�����������ε������ʽ�����DEF�������
��3����EF=a���������������ε�������a��ʾ����DEF�ĸ�PD���г����κ����Ľ���ʽ�����ݶ��κ���������������ֵ��
��� 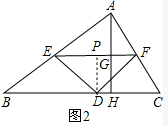 �⣺��1����BC=8����AHΪ4��
�⣺��1����BC=8����AHΪ4��
���ABC�����Ϊ$\frac{1}{2}$��8��4=16��
�ߡ�DEF�ס�ABC��
��$\frac{��DEF�����}{��ABC�����}$=��$\frac{EF}{BC}$��2��
���DEF�������$\frac{9}{4}$��
��2����ͼ2����DP��EF��P��
��DE=DF����EDF=90�㣬
��PD=$\frac{1}{2}$EF��
�������֪���ı���PDHGΪ���Σ���PD=GH��
��EF=x����PD=GH=$\frac{1}{2}$x��
��EF��BC��
��$\frac{EF}{BC}$=$\frac{AG}{AH}$����$\frac{x}{8}$=$\frac{4-\frac{1}{2}x}{4}$��
��ã�x=4��
���DEF�����=$\frac{1}{2}$��EF��PD=4��
��3����ͼ2����EF=a��
��EF��BC��
��$\frac{EF}{BC}$=$\frac{AG}{AH}$����$\frac{a}{8}$=$\frac{4-GH}{4}$��
��ã�GH=4-$\frac{1}{2}$a��
��PD=GH��
���DEF���=$\frac{1}{2}$��a����4-$\frac{1}{2}$a��=-$\frac{1}{2}$��a-4��2+4��
��-$\frac{1}{2}$��0��
�������DEF��������ֵΪ4��
���� ���⿼��������������ε��ж������ʡ����κ����������Լ����ε����ʣ���ȷ���������ߡ����������ص����ʶ����ǽ���Ĺؼ���ע�����������ε�����ȵ������Ʊȵ�ƽ����


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������ijͬѧ����һ��֤�������㽫�����ȱ�ٵ����������ۻ�֤�����ɲ���������
������ijͬѧ����һ��֤�������㽫�����ȱ�ٵ����������ۻ�֤�����ɲ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
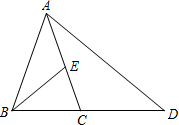 ��֪����ͼ���ڡ�ABC�У�AB=AC=6��BC=4��D�DZ�BC�ӳ�����һ�㣬E�DZ�AC��һ�㣬�ҡ�EBC=��D����CE=x��CD=y��
��֪����ͼ���ڡ�ABC�У�AB=AC=6��BC=4��D�DZ�BC�ӳ�����һ�㣬E�DZ�AC��һ�㣬�ҡ�EBC=��D����CE=x��CD=y���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com