
����Ŀ���۲�̽����������⣮���ı���ABCD�У���E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬˳������E��F��G��H�õ����ı���EFGH�����е��ı��Σ�
��1����ͼ1����֤���е��ı���EFGH��ƽ���ı��Σ�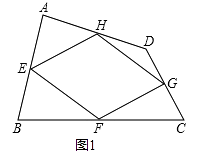
��2������̽������գ�
�ٵ��ı���ABCD���ƽ���ı���ʱ�������е��ı�������
�ڵ��ı���ABCD��ɾ���ʱ�������е��ı�������
�۵��ı���ABCD���������ʱ�������е��ı�������
��3����ͼ2�����е��ı���EFGHΪ����ʱ���Խ���EG��FH�ཻ�ڵ�O��PΪEH�ϵĶ��㣬����P��PM��EG��PN��FH������ֱ�ΪM��N����EF=a��FG=b�����ж�PM+PN�ij��Ƿ�Ϊ��ֵ�����ǣ�����˶�ֵ�������ǣ�˵�����ɣ�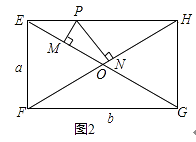
���𰸡�
��1��
�⣺����AC����ͼ1��
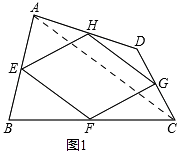
�ڡ�DAC�У�HG��AC����HG= ![]() AC��
AC��
�ڡ�BAC�У�EF��AC����EF= ![]() AC��
AC��
��HG��EF����HG=EF��
���ı���EFGH��ƽ���ı���
��2��ƽ���ı��Σ����Σ�������
��3��
�⣺��ͼ��
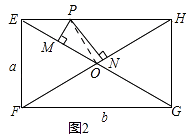
����PO��
�ھ���EFGH�У�EO=HO= ![]() EG=
EG= ![]()
![]() ��
��
��S��EOH= ![]() S�ı���EFGH=
S�ı���EFGH= ![]() ab=S��POE+S��POH��
ab=S��POE+S��POH��
�� ![]() PM��EO+
PM��EO+ ![]() PN��HO=
PN��HO= ![]() ab��
ab��
�� ![]()
![]() ��PM+PN��=
��PM+PN��= ![]() ab��
ab��
��PM+PN= ![]() ��
��
��PM+PN�Ƕ�ֵ
���������⣺ ��2�����ڡ�DAC�У�HG��AC����HG= ![]() AC��
AC��
�ڡ�BAC�У�EF��AC����EF= ![]() AC��
AC��
��HG��EF����HG=EF��
���ı���EFGH��ƽ���ı��Σ�
���Դ���ƽ���ı��Σ�
���ɣ�1���У��ı���EFGH��ƽ���ı��Σ�
ͬ��1���ķ����ã�EH= ![]() BD��
BD��
���ı���ABCD�Ǿ��Σ�
��AC=BD
��EH=EF��
��ƽ���ı���ABCD�����Σ�
���Դ������Σ�
���ɣ�2�����У��ı���EFGH�����Σ�
���ı���ABCD�������Σ�
��AC��BD��
���EFG=90�㣬
������ABCD��������
���Դ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��2����1����4���ĸ����У��ȩ�2С�����ǣ� ��
A.��4
B.��1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڸ����������У��ܻ���ƽ���ı��ε��ǣ�������
A. ��60cmΪһ���Խ��ߣ�20cm��34cmΪ�����ڱ�
B. ��6cm��10cmΪ�����Խ��ߣ�8cmΪһ��
C. ��20cm��36cmΪ�����Խ��ߣ�22cmΪһ��
D. ��6cmΪһ���Խ��ߣ�3cm��10cmΪ�����ڱ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ۽Ǧ��������������Ǻ���ֵ���£�
sin��=sin��180�㩁������cos��=��cos��180�㩁����
��1����sin120�㣬cos120�㣬sin150���ֵ��
��2����һ�������ε������ڽǵı���1��1��4��A��B����������ε��������㣬sinA��cosB�Ƿ���4x2��mx��1=0����������ȵ�ʵ��������m��ֵ����A����B�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��B=32�㣬��AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB �� AC�ڵ�M��N �� �ٷֱ���M �� NΪԲ�ģ����� ![]() MN�ij�Ϊ�뾶�������������ڵ�P �� ����AP���ӳ���BC�ڵ�D �� ������˵����
MN�ij�Ϊ�뾶�������������ڵ�P �� ����AP���ӳ���BC�ڵ�D �� ������˵���� 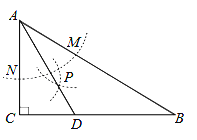
��AD�ǡ�BAC��ƽ���ߣ�
��CD�ǡ�ADC�ĸߣ�
�۵�D��AB�Ĵ�ֱƽ�����ϣ�
�ܡ�ADC=61�㣮
������ȷ���У�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУȥ���ʵ�����ĵ�Ͷ��Ϊ2��Ԫ��Ԥ�ƽ��������Ͷ���ܶ�Ϊ8��Ԫ�������У��������ʵ������Ͷ���ϵ�ƽ��������Ϊx������з��̣�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��(1��m)x��ͼ����������A(x1��y1)��B(x2��y2)���ҵ�x1��x2ʱ��y1��y2����m��ȡֵ��Χ��( )
A. m��0 B. m��0 C. m��1 D. m��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
ijС��Ϊ���ƾ�ס�������ƻ���С������ֲ�ס������ֻ�ľ��6600�ã������ֻ�ľ�����������ֻ�ľ������2����300�ã��ס������ֻ�ľ�������ֱ��Ƕ��ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m>n��km>kn����������Ϊ(����)
A. k>0 B. k<0 C. k��0 D. k��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com