
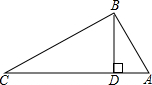
 如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元?
如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元? 分析 首先得出BC2+AB2=122+52=169,AC2=132=169,然后利用其逆定理得到∠ABC=90°确定最短距离,然后利用面积相等求得BD的长,最终求得最低造价.
解答 解:∵BC2+AB2=122+52=169,
AC2=132=169,
∴BC2+AB2=AC2,
∴∠ABC=90°,
当BD⊥AC时BD最短,造价最低,
∵S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BD,
∴BD=$\frac{AB•CB}{AC}$=$\frac{60}{13}$km,
$\frac{60}{13}$×25000=$\frac{1500000}{13}$元.
答:最低造价为$\frac{1500000}{13}$元.
点评 本题考查了勾股定理的应用,利用垂线段最短得出当BD⊥AC时BD最短,造价最低,再利用三角形面积求出是解题关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
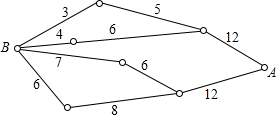 如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( )
如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com