
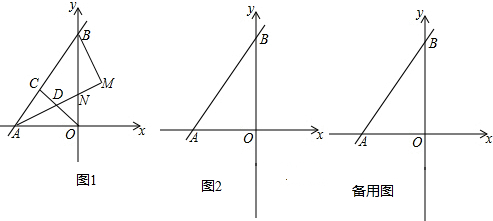
分析 (1)首先根据$\sqrt{{a}^{2}+2ab+{b}^{2}}$+a2b2+4ab+4=0,求出a、b的值各是多少;然后判断出OA=OB,即可判断出△AOB是等腰直角三角形.
(2)首先根据三角形相似的判定方法,判断出△AOD∽△ABN,即可推得$\frac{ON}{BN}=\frac{AO}{AB}$,据此求出ON、BN、AN的值各是多少;然后根据三角形相似的判定方法,判断出△AON∽△BMN,即可判断出$\frac{AN}{BN}=\frac{AO}{BM}$,据此求出$\frac{AN}{BM}$的值是多少即可.
(3)当P点运动时,$\frac{PE}{AQ}$的值不变化.首先根据全等三角形判定的方法,判断出△OAP≌△OBQ,即可判断出OP=OQ;然后根据点E与点B关于x轴对称,可得OE=OB,进一步推得PE=AQ,即可判断出当P点运动时,$\frac{PE}{AQ}$≡1,据此解答即可.
解答 解:(1)∵$\sqrt{{a}^{2}+2ab+{b}^{2}}$+a2b2+4ab+4=0,
∴(a+b)+(ab+2)2=0,
∴$\left\{\begin{array}{l}{a+b=0}\\{ab+2=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\sqrt{2}}\\{b=\sqrt{2}}\end{array}\right.$
∴OA=OB=$\sqrt{2}$,
又∵OA⊥OB,
∴△AOB是等腰直角三角形.
(2)如图1,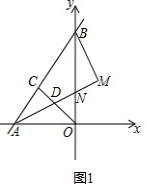 ,
,
∵OA=OB=$\sqrt{2}$,
∴AB=2,
∵OD=0N,
∴∠ODN=∠OND,
∴∠ADO=∠ANB,
∵OA=OB,OC⊥AB,
∴OC是∠AOB的平分线,
∴∠AOD=45°,
又∵∠ABN=45°,
∴∠AOD=∠ABN,
在△AOD和△ABN中,
$\left\{\begin{array}{l}{∠ADO=∠ANB}\\{∠AOD=∠ABN}\end{array}\right.$
∴△AOD∽△ABN,
∴$\frac{OD}{BN}=\frac{AO}{AB}$,
又∵OD=0N,
∴$\frac{ON}{BN}=\frac{AO}{AB}$,
∴$\frac{ON}{\sqrt{2}-ON}=\frac{\sqrt{2}}{2}$,
解得ON=2-$\sqrt{2}$,
∴$BN=OB-ON=\sqrt{2}-(2-\sqrt{2})=2$$\sqrt{2}$-2,
∴AN=$\sqrt{{OA}^{2}{+ON}^{2}}$=$\sqrt{{(\sqrt{2})}^{2}{+(2-\sqrt{2})}^{2}}$=2$\sqrt{2-\sqrt{2}}$.
∵BM⊥AM,
∴∠BMN=90°,
在△AON和△BMN中,
$\left\{\begin{array}{l}{∠AON=∠BMN=90°}\\{∠ANO=∠BNM}\end{array}\right.$
∴△AON∽△BMN,
∴$\frac{AN}{BN}=\frac{AO}{BM}$,
∴BM=$\frac{AO•BN}{AN}$=$\frac{\sqrt{2}×(2\sqrt{2}-2)}{AN}=\frac{4-2\sqrt{2}}{AN}$,
∴$\frac{AN}{BM}$=$\frac{{AN}^{2}}{4-2\sqrt{2}}$=$\frac{8-4\sqrt{2}}{4-2\sqrt{2}}$=2.
(3)当P点运动时,$\frac{PE}{AQ}$的值不变化.
如图2,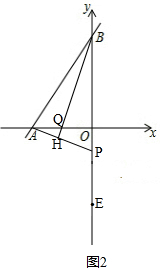 ,
,
∵BH⊥AP,
∴∠BHP=90°,∠HBP+∠HPB=90°,
又∵∠OAP+∠HPB=90°,
∴∠OAP=∠HBP,
∴∠OAP=∠OBQ,
在△OAP和△OBQ中,
$\left\{\begin{array}{l}{∠OAP=∠OBQ}\\{AO=BO}\\{∠AOP=∠BOQ=90°}\end{array}\right.$
∴△OAP≌△OBQ,
∴OP=OQ,
∵点E与点B关于x轴对称,
∴OE=OB,
∴PE=OE-OP=OB-OP=OA-OQ=AQ,
∴$\frac{PE}{AQ}$=1,
即当P点运动时,$\frac{PE}{AQ}$的值不变化,恒为1.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
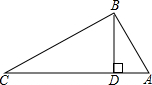 如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元?
如图所示,三个村庄A,B,C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC.已知公路的造价为25000元/km,求修条公路的最低造价是多少元?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
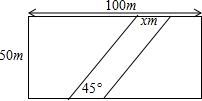 如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.
如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
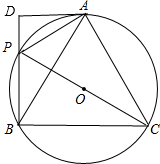 如图,等边△ABC内接于圆O,P是劣弧AB上任意一点,连接PA,PB,PC,过点A作⊙O的切线交BP的延长线于点D.
如图,等边△ABC内接于圆O,P是劣弧AB上任意一点,连接PA,PB,PC,过点A作⊙O的切线交BP的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com