
【题目】下表中给出了变量x,与y=ax2,y=ax2+bx+c之间的部分对应值,(表格中的符号“…”表示该项数据已丢失)
x | ﹣1 | 0 | 1 |
ax2 | … | … | 1 |
ax2+bx+c | 7 | 2 | … |
(1)求抛物线y=ax2+bx+c的表达式
(2)抛物线y=ax2+bx+c的顶点为D,与y轴的交点为A,点M是抛物线对称轴上一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求B点坐标;
(3)在(2)的条件下,设线段BD与x轴交于点C,试写出∠BAD和∠DCO的数量关系,并说明理由.

【答案】(1) y=x2﹣4x+2;(2) 点B的坐标为(5,7);(3)∠BAD和∠DCO互补,理由详见解析.
【解析】
(1)由(1,1)在抛物线y=ax2上可求出a值,再由(﹣1,7)、(0,2)在抛物线y=x2+bx+c上可求出b、c的值,此题得解;
(2)由△ADM和△BDM同底可得出两三角形的面积比等于高的比,结合点A的坐标即可求出点B的横坐标,再利用二次函数图象上点的坐标特征即可求出点B的坐标;
(3)利用二次函数图象上点的坐标特征可求出A、D的坐标,过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,根据点B、D的坐标利用待定系数法可求出直线BD的解析式,利用一次函数图象上点的坐标特征可求出点N的坐标,利用两点间的距离公式可求出BA、BD、BN的长度,由三者间的关系结合∠ABD=∠NBA,可证出△ABD∽△NBA,根据相似三角形的性质可得出∠ANB=∠DAB,再由∠ANB+∠AND=180°可得出∠DAB+∠DCO=180°,即∠BAD和∠DCO互补.
(1)当x=1时,y=ax2=1,
解得:a=1;
将(﹣1,7)、(0,2)代入y=x2+bx+c,得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线的表达式为y=x2﹣4x+2;
(2)∵△ADM和△BDM同底,且△ADM与△BDM的面积比为2:3,
∴点A到抛物线的距离与点B到抛物线的距离比为2:3.
∵抛物线y=x2﹣4x+2的对称轴为直线x=﹣![]() =2,点A的横坐标为0,
=2,点A的横坐标为0,
∴点B到抛物线的距离为3,
∴点B的横坐标为3+2=5,
∴点B的坐标为(5,7).
(3)∠BAD和∠DCO互补,理由如下:
当x=0时,y=x2﹣4x+2=2,
∴点A的坐标为(0,2),
∵y=x2﹣4x+2=(x﹣2)2﹣2,
∴点D的坐标为(2,﹣2).
过点A作AN∥x轴,交BD于点N,则∠AND=∠DCO,如图所示.
设直线BD的表达式为y=mx+n(m≠0),
将B(5,7)、D(2,﹣2)代入y=mx+n,
![]() ,解得:
,解得:![]() ,
,
∴直线BD的表达式为y=3x﹣8.
当y=2时,有3x﹣8=2,
解得:x=![]() ,
,
∴点N的坐标为(![]() ,2).
,2).
∵A(0,2),B(5,7),D(2,﹣2),
∴AB=5![]() ,BD=3
,BD=3![]() ,BN=
,BN=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
又∵∠ABD=∠NBA,
∴△ABD∽△NBA,
∴∠ANB=∠DAB.
∵∠ANB+∠AND=180°,
∴∠DAB+∠DCO=180°,
∴∠BAD和∠DCO互补.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));以此下去,则正方形AnBnCnDn的面积为________.
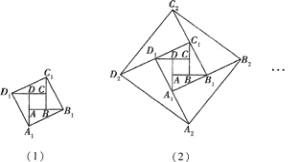
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=![]() ,点E在弧AD上,射线AE与CD的延长线交于点F.
,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
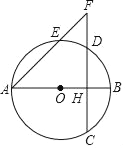
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
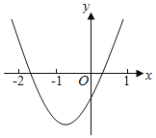
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
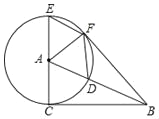
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点P(0,2),以P为圆心,OP为半径的半圆与y轴的另一个交点是C,一次函数![]() (m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
(m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
(1)B点坐标是 (用含m的代数式表示),∠ABO= °.
(2)若点N是直线AB与半圆CO的一个公共点(两个公共点时,N为右侧一点),过点N作⊙P的切线交x轴于点E,如图2.是否存在这样的m的值,使得△EBN是直角三角形.若存在,求出m的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com