
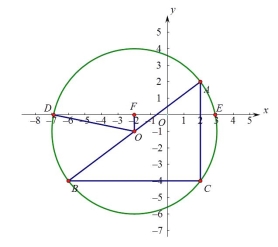
【题目】平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .
【答案】(-2,-1);![]()
【解析】在平面直角坐标中标出点A(2,2),B(-6,-4),C(2,-4),
可得![]() ABC是一个直角三角形,
ABC是一个直角三角形,
所以![]() ABC的外心O是AB的中点,则外心O的坐标为
ABC的外心O是AB的中点,则外心O的坐标为![]() , 即(-2,-1);
, 即(-2,-1);![]()
![]() 作OF
作OF![]() x轴,则外心到x轴的距离是OF=1,且
x轴,则外心到x轴的距离是OF=1,且![]() ABC的外接圆半径为
ABC的外接圆半径为![]() ,
,
则弦长DE=2×![]() .
.
所以答案是(-2,-1);4 ![]() .
.
【考点精析】本题主要考查了圆心角、弧、弦的关系和三角形的外接圆与外心的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1).先化简,再求值:3a2+(4a2-2a-1)-2(3a2-a+1),其中a1![]()
(2). A=3a2+6ab-b2,B=2b2-5ab+a2,C=-4a2-ab+b2,先化简,再求值:A-[B-(A-B+3C)]-(A-B),其中 a=-0.2,b=-0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.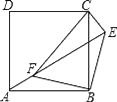
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )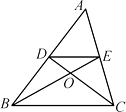
A.DE是△ABC的中位线
B.点O是△ABC的重心
C.△DEO∽△CBO
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B在数轴上表示的数分别是m,n.
(1)填写下表:

(2)若A,B两点间的距离为d,写出d与m,n之间的数量关系.
(3)在数轴上标出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求出所有这些整数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
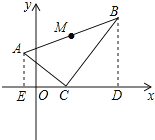
【题目】如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6![]() ,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”; 小华说:“拼成的是矩形”;
小强说:“拼成的是菱形”; 小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
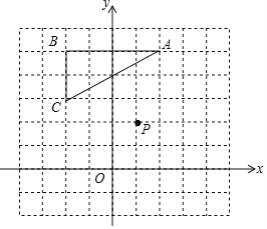
【题目】在如图所示的网格纸中,建立了平面直角坐标系xOy,点P(1,2),点A(2,5),B(-2,5),C(-2,3).
(1)以点P为对称中心,画出△A′B′C′,使△A′B′C′与△ABC关于点P对称,并写出下列点的坐标:B′________,C′________;
(2)多边形ABCA′B′C′的面积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com