
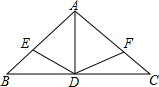
 如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )
如图,在△ABC中,AB=AC,AD是角平分线,点E、F分别在AB、AC上,且BE=CF,则下列说法正确的有( )| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
| 1 |
| 3 |

|
| 1 |
| 3 |


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 用6个大小相同的正方体搭成如图所示的几何体,下列说法正确的是( )
用6个大小相同的正方体搭成如图所示的几何体,下列说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、主视图、俯视图的面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
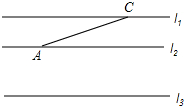 如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1,l2,l3之间的距离为2,点A、C分别在直线l2,l1上,查看答案和解析>>
科目:初中数学 来源: 题型:
 观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )
观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )| A、沿对角线平移到左上角即可得到左上角梅花 |
| B、沿对角线平移到右上角,再顺时针旋转90°可得到右上角梅花 |
| C、沿对角线平移到右下角,再旋转180°可得到右下角梅花 |
| D、沿对角线平移到左下角,再顺时针旋转90°可得到左下角梅花 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com