
【题目】在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
(1)求抛物线的表达式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,N是线段EF上一动点,M(m,0)是x轴上一动点,若∠MNC=90°,直接写出实数m的取值范围.
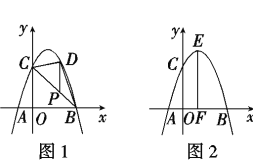
【答案】(1)y=-x2+2x+3;(2)P(![]() ,
,![]() );(3)
);(3)![]()
【解析】
(1)由y=-x2+bx+c经过点A、B、C,A(-1,0),C(0,3),利用待定系数法即可求得此抛物线的解析式;
(2)首先令-x2+2x+3=0,求得点B的坐标,然后设直线BC的解析式为y=kx+b′,由待定系数法即可求得直线BC的解析式,再设P(a,3-a),即可得D(a,-a2+2a+3),即可求得PD的长,由S△BDC=S△PDC+S△PDB,即可得S△BDC=![]() ,利用二次函数的性质,即可求得当△BDC的面积最大时,求点P的坐标;
,利用二次函数的性质,即可求得当△BDC的面积最大时,求点P的坐标;
(3)首先过C作CH⊥EF于H点,则CH=EH=1,然后分别从点M在EF左侧与M在EF右侧时去分析求解即可求得答案.
解:(1)由题![]() ,解得:
,解得:![]() ,
,
所以抛物线表达式为![]()
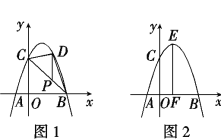
(2)令![]() ,
,
∴![]() .即
.即![]()
设直线![]() 的表达式为
的表达式为![]() ,
,
∴![]()
∴![]()
故直线![]() 的表达式为
的表达式为![]() ,
,
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() 的面积最大,此时
的面积最大,此时![]()
(3)![]() 的取值范围是:
的取值范围是:![]()


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是![]() 小时、
小时、![]() 小时、
小时、![]() 小时、
小时、![]() 小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
A.![]() 小时B.
小时B.![]() 小时C.
小时C.![]() 或
或![]() 小时D.
小时D.![]() 或
或![]() 或
或![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
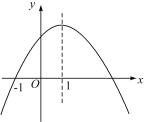
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(-![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com