
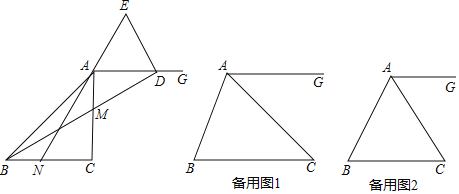
【题目】已知:△ABC是等腰三角形,CA=CB,0°<∠ACB≤90°.点M在边AC上,点N在边BC上(点M、点N不与所在线段端点重合),BN=AM,连接AN,BM,射线AG∥BC,延长BM交射线AG于点D,点E在直线AN上,且AE=DE.
(1)如图,当∠ACB=90°时
①求证:△BCM≌△ACN;
②求∠BDE的度数;
(2)当∠ACB=α,其它多件不变时,∠BDE的度数是 (用含α的代数式表示)
(3)若△ABC是等边三角形,AB=3![]() ,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
,点N是BC边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.
【答案】(1)①证明见解析;②∠BDE=90°;(2)α或180°﹣α;(3)CF的长为![]() 或4
或4![]() .
.
【解析】(1)①根据SAS证明即可;
②想办法证明∠ADE+∠ADB=90°即可;
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上时,②如图3中,当点E在NA的延长线上时,
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,解直角三角形即可.②如图5中,当CN=
时,作AK⊥BC于K,解直角三角形即可.②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,结合图形求解即可.
时,作AK⊥BC于K,DH⊥BC于H,结合图形求解即可.
(1)①如图1中,
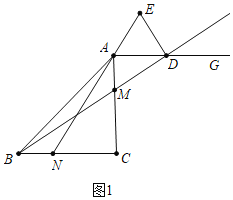
∵CA=CB,BN=AM,
∴CB﹣BN=CA﹣AM,
即CN=CM,
∵∠ACN=∠BCM,
∴△BCM≌△CAN;
②如图1中,
∵△BCM≌△ACN,
∴∠MBC=∠NAC,
∵EA=ED,
∴∠EAD=∠EDA,
∵AG∥BC,
∴∠GAC=∠ACB=90°,∠ADB=∠DBC,
∴∠ADB=∠NAC,
∴∠ADB+∠EDA=∠NAC+∠EAD,
∵∠ADB+∠EDA=180°﹣90°=90°,
∴∠BDE=90°;
(2)如图2中,当点E在AN的延长线上时,
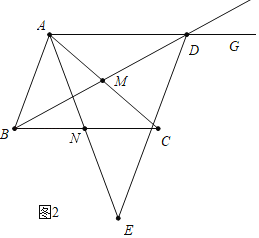
易证:∠CBM=∠ADB=∠CAN,∠ACB=∠CAD,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠CAN+∠CAD=∠BDE+∠ADB,
∴∠BDE=∠ACB=α;
如图3中,当点E在NA的延长线上时,
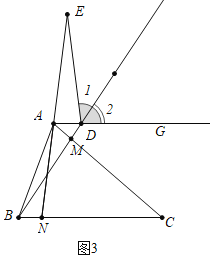
易证:∠1+∠2=∠CAN+∠DAC,
∵∠2=∠ADM=∠CBD=∠CAN,
∴∠1=∠CAD=∠ACB=α,
∴∠BDE=180°﹣α,
综上所述,∠BDE=α或180°﹣α,
故答案为:α或180°﹣α;
(3)如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,
时,作AK⊥BC于K,
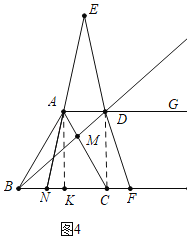
∵AD∥BC,
∴![]() ,
,
∴AD=![]() ,AC=3
,AC=3![]() ,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,
,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,
∴CF=NK=BK﹣BN=![]() ﹣
﹣![]() =
=![]() ;
;
如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H,
时,作AK⊥BC于K,DH⊥BC于H,
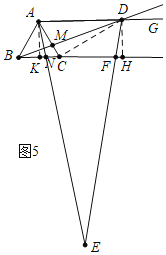
∵AD∥BC,
∴![]() ,
,
∴AD=6![]() ,易证△ACD是直角三角形,
,易证△ACD是直角三角形,
由△ACK∽△CDH,可得CH=![]() AK=
AK=![]() ,
,
由△AKN≌△DHF,可得KN=FH=![]() ,
,
∴CF=CH﹣FH=4![]() .
.
综上所述,CF的长为![]() 或4
或4![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
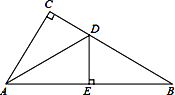
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“幸运数”;如果一个正整数
为“幸运数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“幸运数”,且
为“幸运数”,且![]() 的三十三分之一是完全平方数,则符合条件的最大一个
的三十三分之一是完全平方数,则符合条件的最大一个![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
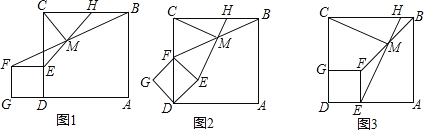
【题目】如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.
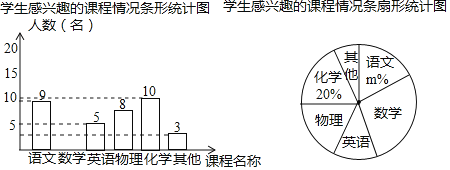
据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生,m的值是 .
(2)请根据据以上信息直在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
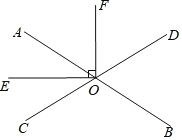
【题目】如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
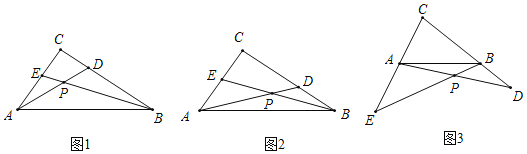
【题目】已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:
(1)如图1,若k=1,则∠APE的度数为 ;
(2)如图2,若k=![]() ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.
,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.
(3)如图3,若k=![]() ,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.
,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若![]() ,
,![]() ,
,![]() 为数轴上三点且点
为数轴上三点且点![]() 在
在![]() ,
,![]() 之间,若点
之间,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的3倍,我们就称点
的距离的3倍,我们就称点![]() 是
是![]() 的好点.
的好点.
如图1,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为2.表示1的点
表示的数为2.表示1的点![]() 到
到![]() 的距离是3,到
的距离是3,到![]() 的距离是1,那么点
的距离是1,那么点![]() 是
是![]() 的好点;又如,表示
的好点;又如,表示![]() 的点
的点![]() 到
到![]() 的距离是1,到
的距离是1,到![]() 的距离是3,那么点
的距离是3,那么点![]() 就不是
就不是![]() 的好点,但点
的好点,但点![]() 是
是![]() 的好点.
的好点.
知识运用:
(1)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为2.
所表示的数为2.
数 所表示的点是![]() 的好点;
的好点;
数 所表示的点是![]() 的好点;
的好点;
(2)若点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 的右边,且点
的右边,且点![]() 在
在![]() ,
,![]() 之间,点
之间,点![]() 是
是![]() 的好点,求点
的好点,求点![]() 所表示的数(用含
所表示的数(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() 、
、![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为27,现有一只电子蚂蚁
所表示的数为27,现有一只电子蚂蚁![]() 从点
从点![]() 出发,以每秒6个单位的速度向右运动,运动时间为
出发,以每秒6个单位的速度向右运动,运动时间为![]() 秒.如果
秒.如果![]() ,
,![]() ,
,![]() 中恰有一个点为其余两点的好点,求
中恰有一个点为其余两点的好点,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).当t为__________ 时,以B,P,Q三点为顶点的三角形是等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com