
ЁОЬтФПЁПвбжЊRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЕуDЁЂEЗжБ№дкBCЁЂACБпЩЯЃЌСЌНсBEЁЂADНЛгкЕуPЃЌЩшAC=kBDЃЌCD=kAEЃЌkЮЊГЃЪ§ЃЌЪдЬНОПЁЯAPEЕФЖШЪ§ЃК
ЃЈ1ЃЉШчЭМ1ЃЌШєk=1ЃЌдђЁЯAPEЕФЖШЪ§ЮЊ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєk=![]() ЃЌЪдЮЪЃЈ1ЃЉжаЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧѓГіЁЯAPEЕФЖШЪ§ЃЎ
ЃЌЪдЮЪЃЈ1ЃЉжаЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧѓГіЁЯAPEЕФЖШЪ§ЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌШєk=![]() ЃЌЧвDЁЂEЗжБ№дкCBЁЂCAЕФбгГЄЯпЩЯЃЌЃЈ2ЃЉжаЕФНсТлЪЧЗёГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЌЧвDЁЂEЗжБ№дкCBЁЂCAЕФбгГЄЯпЩЯЃЌЃЈ2ЃЉжаЕФНсТлЪЧЗёГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
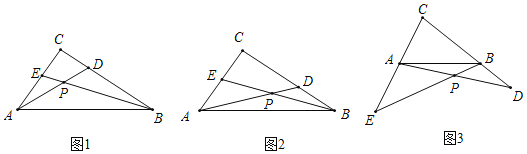
ЁОД№АИЁПЃЈ1ЃЉ45ЁуЃЛЃЈ2ЃЉЃЈ1ЃЉжаНсТлВЛГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉЃЈ2ЃЉжаНсТлГЩСЂЃЌРэгЩМћНтЮі.
ЁОНтЮіЁПЃЈ1ЃЉЯШХаЖЯГіЫФБпаЮADBFЪЧЦНааЫФБпаЮЃЌЕУГіBD=AFЃЌBF=ADЃЌНјЖјХаЖЯГіЁїFAEЁеЁїACDЃЌЕУГіEF=AD=BFЃЌдйХаЖЯГіЁЯEFB=90ЁуЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШХаЖЯГіЫФБпаЮADBFЪЧЦНааЫФБпаЮЃЌЕУГіBD=AFЃЌBF=ADЃЌНјЖјХаЖЯГіЁїFAEЁзЁїACDЃЌдйХаЖЯГіЁЯEFB=90ЁуЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіЫФБпаЮADBFЪЧЦНааЫФБпаЮЃЌЕУГіBD=AFЃЌBF=ADЃЌНјЖјХаЖЯГіЁїACDЁзЁїHEAЃЌдйХаЖЯГіЁЯEFB=90ЁуЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуAзїAFЁЮCBЃЌЙ§ЕуBзїBFЁЮADЯрНЛгкFЃЌСЌНгEFЃЌ
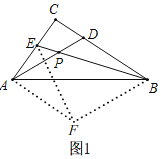
ЁрЁЯFBE=ЁЯAPEЃЌЁЯFAC=ЁЯC=90ЁуЃЌЫФБпаЮADBFЪЧЦНааЫФБпаЮЃЌ
ЁрBD=AFЃЌBF=ADЃЎ
ЁпAC=BDЃЌCD=AEЃЌ
ЁрAF=ACЃЎ
ЁпЁЯFAC=ЁЯC=90ЁуЃЌ
ЁрЁїFAEЁеЁїACDЃЌ
ЁрEF=AD=BFЃЌЁЯFEA=ЁЯADCЃЎ
ЁпЁЯADC+ЁЯCAD=90ЁуЃЌ
ЁрЁЯFEA+ЁЯCAD=90Ёу=ЁЯEHDЃЎ
ЁпADЁЮBFЃЌ
ЁрЁЯEFB=90ЁуЃЎ
ЁпEF=BFЃЌ
ЁрЁЯFBE=45ЁуЃЌ
ЁрЁЯAPE=45ЁуЃЎ
ЃЈ2ЃЉЃЈ1ЃЉжаНсТлВЛГЩСЂЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌЙ§ЕуAзїAFЁЮCBЃЌЙ§ЕуBзїBFЁЮADЯрНЛгкFЃЌСЌНгEFЃЌ
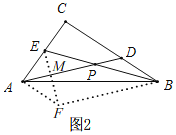
ЁрЁЯFBE=ЁЯAPEЃЌЁЯFAC=ЁЯC=90ЁуЃЌЫФБпаЮADBFЪЧЦНааЫФБпаЮЃЌ
ЁрBD=AFЃЌBF=ADЃЎ
ЁпAC=![]() BDЃЌCD=
BDЃЌCD=![]() AEЃЌ
AEЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпBD=AFЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпЁЯFAC=ЁЯC=90ЁуЃЌ
ЁрЁїFAEЁзЁїACDЃЌ
Ёр![]() ЃЌЁЯFEA=ЁЯADCЃЎ
ЃЌЁЯFEA=ЁЯADCЃЎ
ЁпЁЯADC+ЁЯCAD=90ЁуЃЌ
ЁрЁЯFEA+ЁЯCAD=90Ёу=ЁЯEMDЃЎ
ЁпADЁЮBFЃЌ
ЁрЁЯEFB=90ЁуЃЎ
дкRtЁїEFBжаЃЌtanЁЯFBE=![]() ЃЌ
ЃЌ
ЁрЁЯFBE=30ЁуЃЌ
ЁрЁЯAPE=30ЁуЃЌ
ЃЈ3ЃЉЃЈ2ЃЉжаНсТлГЩСЂЃЌШчЭМ3ЃЌзїEHЁЮCDЃЌDHЁЮBEЃЌEHЃЌDHЯрНЛгкHЃЌСЌНгAHЃЌ
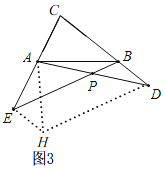
ЁрЁЯAPE=ЁЯADHЃЌЁЯHEC=ЁЯC=90ЁуЃЌЫФБпаЮEBDHЪЧЦНааЫФБпаЮЃЌ
ЁрBE=DHЃЌEH=BDЃЎ
ЁпAC=![]() BDЃЌCD=
BDЃЌCD=![]() AEЃЌ
AEЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпЁЯHEA=ЁЯC=90ЁуЃЌ
ЁрЁїACDЁзЁїHEAЃЌ
Ёр![]() ЃЌЁЯADC=ЁЯHAEЃЎ
ЃЌЁЯADC=ЁЯHAEЃЎ
ЁпЁЯCAD+ЁЯADC=90ЁуЃЌ
ЁрЁЯHAE+ЁЯCAD=90ЁуЃЌ
ЁрЁЯHAD=90ЁуЃЎ
дкRtЁїDAHжаЃЌtanЁЯADH=![]() ЃЌ
ЃЌ
ЁрЁЯADH=30ЁуЃЌ
ЁрЁЯAPE=30ЁуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§дкИФдьЕФШЫааЕРЙЄЕиЩЯЃЌгаСНжжЦЬЩшТЗУцВФСЯЃКвЛжжЪЧГЄЮЊacmЁЂПэЮЊbcmЕФОиаЮАхВФЃЈШчЭМ1ЃЉЃЌСэвЛжжЪЧБпГЄЮЊccmЕФе§ЗНаЮЕизЉЃЈШчЭМ2ЃЉЃЎ
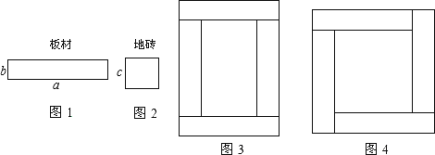
ЃЈ1ЃЉгУЖрЩйПщШчЭМ2ЫљЪОЕФе§ЗНаЮЕизЉФмЦДГівЛИіаТЕФе§ЗНаЮЃПЃЈжЛвЊаДГівЛИіЗћКЯЬѕМўЕФД№АИМДПЩЃЉЃЌВЂаДГіаТе§ЗНаЮЕФУцЛ§ЃЛ
ЃЈ2ЃЉЯжгУШчЭМ1ЫљЪОЕФЫФПщОиаЮАхВФЦЬГЩвЛИіДѓОиаЮЃЈШчЭМ3ЃЉЛђДѓе§ЗНаЮЃЈШчЭМ4ЃЉЃЌжаМфЗжБ№ПеГівЛИіаЁОиаЮКЭвЛИіаЁе§ЗНаЮЃЎ
ЂйЪдБШНЯжаМфЕФаЁОиаЮКЭжаМфЕФаЁе§ЗНаЮЕФУцЛ§ФФИіДѓЃПДѓЖрЩйЃП
ЂкШчЭМ4ЃЌвбжЊДѓе§ЗНаЮЕФБпГЄБШжаМфаЁе§ЗНаЮЕФБпГЄЖр20cmЃЌУцЛ§Дѓ3200cm2ЃЎШчЙћбЁгУШчЭМ2ЫљЪОЕФе§ЗНаЮЕизЉЃЈБпГЄЮЊ20cmЃЉЦЬЩшЭМ4жаМфЕФаЁе§ЗНаЮВПЗжЃЌФЧУДФмЗёзіЕНВЛгУЧаИюЕизЉОЭПЩжБНгУмЦЬЃЈЗьЯЖКіТдВЛМЦЃЉФиЃПШєФмЃЌЧыЧѓГіУмЦЬЫљашЕизЉЕФПщЪ§ЃЛШєВЛФмЃЌжСЩйвЊЧаИюМИПщШчЭМ2ЕФЕизЉЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABEЁЂЁїADCКЭЁїABCЗжБ№ЪЧЙигкABЃЌACБпЫљдкжБЯпЕФжсЖдГЦЭМаЮЃЌШєЁЯ1ЃКЁЯ2ЃКЁЯ3=7ЃК2ЃК1ЃЌдђЁЯІСЕФЖШЪ§ЮЊЃЈЁЁ ЁЁЃЉЃЎ

A.126ЁуB.110ЁуC.108ЁуD.90Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
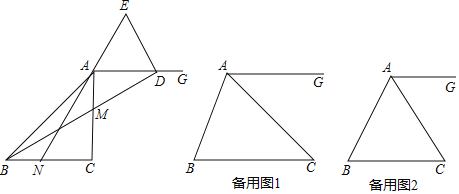
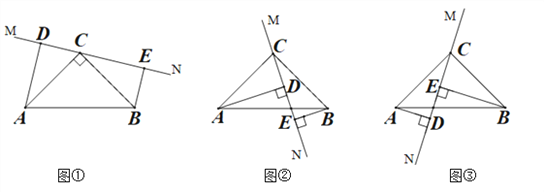
ЁОЬтФПЁПвбжЊЃКЁїABCЪЧЕШбќШ§НЧаЮЃЌCA=CBЃЌ0ЁуЃМЁЯACBЁм90ЁуЃЎЕуMдкБпACЩЯЃЌЕуNдкБпBCЩЯЃЈЕуMЁЂЕуNВЛгыЫљдкЯпЖЮЖЫЕужиКЯЃЉЃЌBN=AMЃЌСЌНгANЃЌBMЃЌЩфЯпAGЁЮBCЃЌбгГЄBMНЛЩфЯпAGгкЕуDЃЌЕуEдкжБЯпANЩЯЃЌЧвAE=DEЃЎ
ЃЈ1ЃЉШчЭМЃЌЕБЁЯACB=90ЁуЪБ
ЂйЧѓжЄЃКЁїBCMЁеЁїACNЃЛ
ЂкЧѓЁЯBDEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЕБЁЯACB=ІСЃЌЦфЫќЖрМўВЛБфЪБЃЌЁЯBDEЕФЖШЪ§ЪЧЁЁ ЁЁЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ3ЃЉШєЁїABCЪЧЕШБпШ§НЧаЮЃЌAB=3![]() ЃЌЕуNЪЧBCБпЩЯЕФШ§ЕШЗжЕуЃЌжБЯпEDгыжБЯпBCНЛгкЕуFЃЌЧыжБНгаДГіЯпЖЮCFЕФГЄЃЎ
ЃЌЕуNЪЧBCБпЩЯЕФШ§ЕШЗжЕуЃЌжБЯпEDгыжБЯпBCНЛгкЕуFЃЌЧыжБНгаДГіЯпЖЮCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃАЫФъМЖМзЁЂввСНАрИїгабЇЩњ50ШЫЃЌЮЊСЫСЫНтетСНИіАрбЇЩњЩэЬхЫижЪЧщПіЃЌНјааСЫГщбљЕїВщЃЌЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
ЃЈ1ЃЉЪеМЏЪ§Он
ДгМзЁЂввСНИіАрИїЫцЛњГщШЁ10УћбЇЩњНјааЩэЬхЫижЪВтЪдЃЌВтЪдГЩМЈЃЈАйЗжжЦЃЉШчЯТЃК
МзАр65 75 75 80 60 50 75 90 85 65
ввАр90 55 80 70 55 70 95 80 65 70
ЃЈ2ЃЉећРэУшЪіЪ§Он
АДШчЯТЗжЪ§ЖЮећРэЁЂУшЪіетСНзщбљБОЪ§ОнЃК

дкБэжаЃКm= ЃЌn= ЃЎ
ЃЈ3ЃЉЗжЮіЪ§Он
ЂйСНзщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчБэЫљЪОЃК

дкБэжаЃКx= ЃЌy= ЃЎ
ЂкШєЙцЖЈВтЪдГЩМЈдк80ЗжЃЈКЌ80ЗжЃЉвдЩЯЕФа№ЪіЩэЬхЫижЪЮЊгХауЃЌЧыЙРМЦввАр50УћбЇЩњжаЩэЬхЫижЪЮЊгХауЕФбЇЩњга ШЫЃЎ
ЂлЯжДгМзАржИЖЈЕФ2УћбЇЩњЃЈ1Фа1ХЎЃЉЃЌввАржИЖЈЕФ3УћбЇЩњЃЈ2Фа1ХЎЃЉжаЗжБ№ГщШЁ1УћбЇЩњШЅВЮМгЩЯМЖВПУХзщжЏЕФЩэЬхЫижЪВтЪдЃЌгУЪїзДЭМКЭСаБэЗЈЧѓГщЕНЕФ2УћЭЌбЇЪЧ1Фа1ХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЯжгадкаЃбЇЩњ2150ШЫЃЌЮЊСЫНтИУаЃбЇЩњЕФПЮгрЛюЖЏЧщПіЃЌВЩШЁЫцЛњГщбљЕФЗНЗЈДгдФЖСЁЂдЫЖЏЁЂгщРжЁЂЦфЫќЫФИіЗНУцЕїВщСЫШєИЩУћбЇЩњЃЌВЂНЋЕїВщЕФНсЙћЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
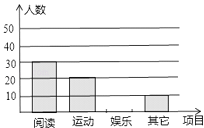
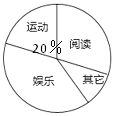
ЃЈ1ЃЉБОДЮЕїВщЙВГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉЭЈЙ§МЦЫуВЙШЋЬѕаЮЭМЃЌВЂЧѓГіЩШаЮЭГМЦЭМжадФЖСВПЗждВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЧыФуЙРМЦИУжабЇдкПЮгрЪБМфВЮМгдФЖСКЭЦфЫќЛюЖЏЕФбЇЩњвЛЙВгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПеХРЯЪІдЊЕЉНкЦкМфЕНЮфЩЬжкдВЩЬГЁЙКТђвЛЬЈФГЦЗХЦБЪМЧБОЕчФдЃЌЧЁЗъЩЬГЁе§ЭЦГіЁАгдЊЕЉЁБДйЯњДђелЛюЖЏЃЌОпЬхгХЛнЧщПіШчБэЃК
ЙКЮязмН№ЖюЃЈдМлЃЉ | елПл |
ВЛГЌЙ§5000дЊЕФВПЗж | ОХел |
ГЌЙ§5000дЊЧвВЛГЌЙ§10000дЊЕФВПЗж | АЫел |
ГЌЙ§10000дЊЧвВЛГЌЙ§20000дЊЕФВПЗж | Цпел |
ЁЁ | ЁЁ |
Р§ШчЃКШєЙКТђЕФЩЬЦЗдМлЮЊ15000дЊЃЌЪЕМЪИЖПюН№ЖюЮЊЃК
5000ЁС90%+ЃЈ10000Љ5000ЃЉЁС80%+ЃЈ15000Љ10000ЃЉЁС70%ЃН12000дЊЃЎ
ЃЈ1ЃЉШєетжжЦЗХЦЕчФдЕФдМлЮЊ8000дЊ/ЬЈЃЌЧыЧѓГіеХРЯЪІЪЕМЪИЖПюН№ЖюЃЛ
ЃЈ2ЃЉвбжЊеХРЯЪІЙКТђвЛЬЈИУЦЗХЦЕчФдЪЕМЪИЖЗб5700дЊЃЎ
ЂйЧѓИУЦЗХЦЕчФдЕФдМлЪЧЖрЩйдЊ/ЬЈЃП
ЂкШєЪлГіетЬЈЕчФдЩЬГЁШдПЩЛёРћ14%ЃЌЧѓетжжЦЗХЦЕчФдЕФНјМлЮЊЖрЩйдЊ/ЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙДЙЩЖЈРэa2+b2=c2БОЩэОЭЪЧвЛИіЙигкaЃЌbЃЌcЕФЗНГЬЃЌТњзуетИіЗНГЬЕФе§ећЪ§НтЃЈaЃЌbЃЌcЃЉЭЈГЃНазіЙДЙЩЪ§зщ.БЯДяИчРЫЙбЇХЩЬсГіСЫвЛИіЙЙдьЙДЙЩЪ§зщЕФЙЋЪНЃЌИљОнИУЙЋЪНПЩвдЙЙдьГіШчЯТЙДЙЩЪ§зщЃКЃЈ3ЃЌ4ЃЌ5ЃЉЃЌЃЈ5ЃЌ12ЃЌ13ЃЉЃЌЃЈ7ЃЌ24ЃЌ25ЃЉЃЌЁ.ЗжЮіЩЯУцЙДЙЩЪ§зщПЩвдЗЂЯжЃЌ4=1ЁСЃЈ3+1ЃЉЃЌ12=2ЁСЃЈ5+1ЃЉЃЌ24=3ЁСЃЈ7+1ЃЉЃЌЁЗжЮіЩЯУцЙцТЩЃЌЕк5ИіЙДЙЩЪ§зщЮЊ_____.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкE.
(1)ЕБжБЯпMNШЦЕуCа§зЊЕНЭМЂйЮЛжУЪБЃЌЧѓжЄЃКDE=AD+BEЃЛ
(2)ЕБжБЯпMNШЦЕуCа§зЊЕНЭМЂкЮЛжУЪБЃЌЪдЮЪЃКDEЃЌADЃЌBEгадѕбљЕФЕШСПЙиЯЕЃПЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУї.
(3)ЕБжБЯпMNШЦЕуCа§зЊЕНЭМЂлЮЛжУЪБЃЌDEЃЌADЃЌBEжЎМфЕФЕШСПЙиЯЕЪЧ (жБНгаДГіД№АИЃЌВЛашжЄУї.)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com