
【题目】正在改造的人行道工地上,有两种铺设路面材料:一种是长为acm、宽为bcm的矩形板材(如图1),另一种是边长为ccm的正方形地砖(如图2).
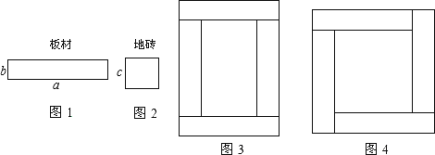
(1)用多少块如图2所示的正方形地砖能拼出一个新的正方形?(只要写出一个符合条件的答案即可),并写出新正方形的面积;
(2)现用如图1所示的四块矩形板材铺成一个大矩形(如图3)或大正方形(如图4),中间分别空出一个小矩形和一个小正方形.
①试比较中间的小矩形和中间的小正方形的面积哪个大?大多少?
②如图4,已知大正方形的边长比中间小正方形的边长多20cm,面积大3200cm2.如果选用如图2所示的正方形地砖(边长为20cm)铺设图4中间的小正方形部分,那么能否做到不用切割地砖就可直接密铺(缝隙忽略不计)呢?若能,请求出密铺所需地砖的块数;若不能,至少要切割几块如图2的地砖?
【答案】(1)4个,![]() (2)①小正方形大,
(2)①小正方形大,![]() ②不能,4块
②不能,4块
【解析】
(1)根据正方形的性质和正方形的边长解答;
(2)①列出图形的面积表达式,再进行比较;②根据图形的特点,以求得a、b的长.
解:(1)将四个图2所示的正方形拼成一个新正方形即可

其面积为![]() ;(该小题答案不唯一);
;(该小题答案不唯一);
(2)①在图3中,小矩形的面积为![]() 在图4中,小正方形的面积为
在图4中,小正方形的面积为![]()
∵![]() >0 ∴
>0 ∴![]() <
<![]()
∴小正方形的面积比小矩形的面积大![]() .
.
②(法一):
图4中大正方形的边长比中间小正方形的边长多20cm,故b=20÷2=10cm; 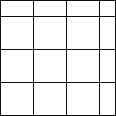
由图4中大正方形的边长比中间小正方形的面积大3200cm2得,4ab=3200,
又∵b=10cm,
∴a=3200÷(4×10)=80cm.
则图4中中间小正方形的边长为80-10=70cm.
如右图至少要切割4块如图2的地砖.
(法二)②依题意,得 :![]()
解得:![]()
∴图4中小正方形的边长为70 cm,面积为4900![]()
∵![]()
∴不能,至少要切割4块如图2的地砖.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
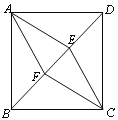
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如果![]() ,
,![]() 且
且![]() ,求
,求![]() 的值.
的值.
(2)数轴上表示3和5的两点距离是 .表示 -3和一5两点的距离是 .表示 3和-5两点的距离是 .
(3)在数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 的距离是 ;(用含
的距离是 ;(用含![]() 的代数式表示)如果
的代数式表示)如果![]() ,那么
,那么![]() .
.
(4)猜想对于有理数![]() ,
,![]() 能够取得的最小值是 .
能够取得的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
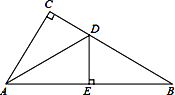
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,∠A=∠D=∠B=∠C=90,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm.

(1)求证:AF=DE.
(2)若AD+DC=18,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
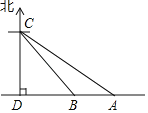
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
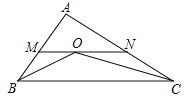
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“幸运数”;如果一个正整数
为“幸运数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“幸运数”,且
为“幸运数”,且![]() 的三十三分之一是完全平方数,则符合条件的最大一个
的三十三分之一是完全平方数,则符合条件的最大一个![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:
(1)如图1,若k=1,则∠APE的度数为 ;
(2)如图2,若k=![]() ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.
,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.
(3)如图3,若k=![]() ,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.
,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.
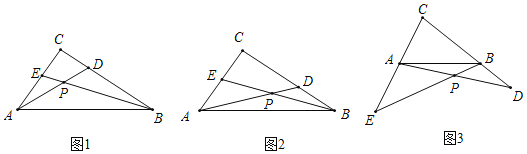
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com