
����Ŀ�����Ž�ͨ��·�IJ������ƣ�����������ҵ�ķ�չ��ij��ij���ξ�����A��B��C��D��E���������㣬�������β���ͳ�ƻ��Ƴ�2018����ʮ��һ�������ڼ��������ͳ��ͼ������������Ϣ����������⣺
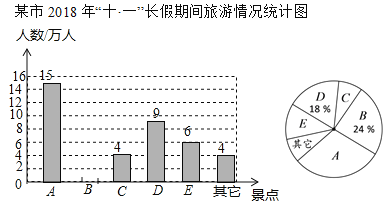
�� 2018����ʮ��һ���ڼ䣬���д����ξ������Ӵ��ο� ���ˣ�����ͳ��ͼ��A��������Ӧ��Բ�ĽǵĶ����� ��
�� ��ȫ����ͳ��ͼ��
�� ���ݽ����굽�������������������ƣ�Ԥ��2019����ʮ��һ���ڽ���80���ο�ѡ��������Σ�������ж������˻�ѡ��ȥE�������Σ�
���𰸡��� 50��108�� ���Ƽ������� �� 9.6����.
��������
��1������A����������Լ��ٷֱȽ��м��㼴�ɵõ������ܱ߾��㹲�Ӵ��ο����������A��������Ӧ��Բ�ĽǵĶ������ٸ�������Բ�ĽǵĶ���=����ռ����İٷֱ���360�����м��㼴�ɣ�
��2�����B����Ӵ��ο��������ɲ�ȫ����ͳ��ͼ��
��3��������ȥ�������弴�ɵý�.
��1�������ܱ߾��㹲�Ӵ��ο���Ϊ��15��30%=50�����ˣ���
A��������Ӧ��Բ�ĽǵĶ����ǣ�30%��360��=108����
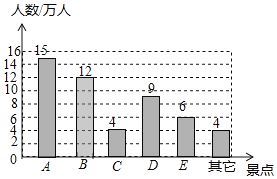
��2��B����Ӵ��ο���Ϊ��50��24%=12�����ˣ���
��ȫ����ͳ��ͼ���£�
�� ![]() �����ˣ�
�����ˣ�
�𣺹�����9.6���˻�ѡ��ȥE��������.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ�ѧ����������չ��ijУ��֯��չ�����Ż���ֱ������������ࡢ�����ࡢ��ѧ�༰���������ţ�Ҫ�����˲������ţ�ÿ��ֻ��ѡ��һ���Ϊ�˽�ѧ��ϲ���������Ż��ѧУ����һ�γ������飮�����ռ��������ݣ����Ƴ�����������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
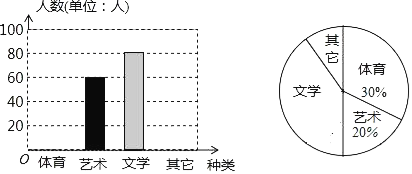
��1���˴ι������˶����ˣ�
��2������������������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
��4������У��3000��ѧ���������ϲ����ѧ�����ŵ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
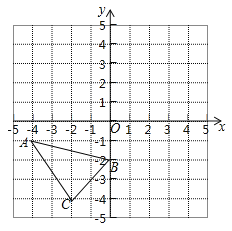
����Ŀ����ͼ����ABC���������㶼�ڱ߳�Ϊ1��С��������ɵ�����ĸ���ϣ��Ե�OΪԭ�㽨��ֱ������ϵ���ش��������⣺
��1������ABC������ƽ��5����λ��������ƽ��1����λ�õ���A1B1C1��������A1B1C1����ֱ��д��A1�������� ����
��2������A1B1C1�Ƶ㣨0����1��˳ʱ����ת90��õ���A2B2C2������A2B2C2��
��3���۲�ͼ�η��֣�A2B2C2������ABC�Ƶ��� ��˳ʱ����ת�� ���ȵõ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ������С������ֱ��������3��4��5����ЩС������ֲ�ͬ���������ͬ��
��1���ӿڴ����������һ��С��С���ϵ�������ż���ĸ�����______��
��2���ӿڴ����������һ��С�������ֺ�Żأ����������һ��С�������֣����û���״ͼ�����б����ķ�����������������С���ϵ����ֶ��������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺
���⣺����ƽ���ڣ���֪�ֱ���2���㣬3���㣬4���㣬5���㣬����![]() ���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
̽����Ϊ�˽��������⣬ϣ��С���ͬѧ�ǣ���������±������̽������Ϊ�˷����о����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���� | 2 | 3 | 4 | 5 | �� |
|
ʾ��ͼ |
|
|
|
| �� |
|
ֱ������ | 1 |
|
|
| �� |
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ����������ʱ��ֱ������Ϊ______��
��2����ijͬѧ���ձ����еķ�����������28��ֱ�ߣ����ƽ�����ж��ٸ���֪�㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ABΪ��ԲO��ֱ�����뾶OP��AB�����ӻ�AP��һ��D��DC��AB�ڵ�C������DB����OP�ڵ�E����DBA��22.5����
�� ��OC��2����AC�ij�����������
�� ��д��AC��PE֮���������ϵ����˵�����ɣ�
�� ����AD���ӳ�����OP���ӳ����ڵ�G����DC��x��GP��y�������x��y֮��ĵ�����ϵʽ. �����Ȳ�ȫͼ�Σ��ٽ��
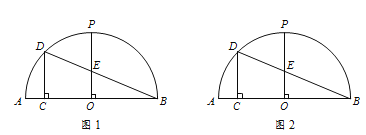
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x��2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н�����ȷ���ǣ�������
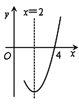
A.��x��2ʱ��y��x���������B.a��b��c��0
C.�����߹��㣨��4��0��D.4a��b��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
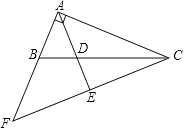
����Ŀ��ֱ��������ABC�У�![]() ��D��б��BC��һ�㣬��
��D��б��BC��һ�㣬��![]() ������C��
������C��![]() ����AD���ӳ����ڵ�E����AB�ӳ����ڵ�F��
����AD���ӳ����ڵ�E����AB�ӳ����ڵ�F��
![]() ��֤��
��֤��![]() ��
��
![]() ��
��![]() ��
��![]() ������B��
������B��![]() �ڵ�G������
�ڵ�G������![]() �����ⲹȫͼ�Σ������ı���ABGD�������
�����ⲹȫͼ�Σ������ı���ABGD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬AB=4������P�ӵ�A��������AB��ÿ��2����λ���ȵ��ٶ����յ�B�˶�������P��PD��AC�ڵ�D����P�����A��B�غϣ�������DPQ=60������PQ������DC�ڵ�Q�����P���˶�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾ�߶�DC�ij���
��2������Q���C�غ�ʱ����t��ֵ��
��3�����PDQ���ABC�ص�����ͼ�ε����ΪS����S��t֮��ĺ�����ϵʽ��
��4�����߶�PQ�Ĵ�ֱƽ���߾�����ABCһ���е�ʱ��ֱ��д��t��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com