
ЁОЬтФПЁПФГГізтГЕМнЪЛдБДгЙЋЫОГіЗЂЃЌдкФЯББЯђЕФШЫУёТЗЩЯСЌајНгЫЭ5ХњПЭШЫЃЌааЪЛТЗГЬМЧТМШчЯТЃЈЙцЖЈЯђФЯЮЊе§ЃЌЯђББЮЊИКЃЌЕЅЮЛЃК![]() ЃЉЃК
ЃЉЃК
Ек1Хњ | Ек2Хњ | Ек3Хњ | Ек4Хњ | Ек5Хњ |
|
|
|
|
|
ЃЈ1ЃЉНгЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБдкЙЋЫОЪВУДЗНЯђЃЌОрРыЙЋЫОЖрдЖЃП
ЃЈ2ЃЉШєИУГізтГЕЕФЪеЗбБъзМЮЊЃКааЪЛТЗГЬВЛГЌЙ§![]() ЃЌЪеЗб10дЊЃЛГЌЙ§
ЃЌЪеЗб10дЊЃЛГЌЙ§![]() ЃЌЖдГЌЙ§ВПЗжСэМгЪеУПЧЇУз1.8дЊ.ЕБЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБЙВЪеЕНГЕЗбЖрЩйдЊЃП
ЃЌЖдГЌЙ§ВПЗжСэМгЪеУПЧЇУз1.8дЊ.ЕБЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБЙВЪеЕНГЕЗбЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉИУМнЪЛдБдкЙЋЫОФЯБпЃЌОрРыЙЋЫО![]() ЃЛЃЈ2ЃЉЕБЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБЙВЪеЕНГЕЗб68дЊ.
ЃЛЃЈ2ЃЉЕБЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБЙВЪеЕНГЕЗб68дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнгаРэЪ§МгЗЈМДПЩЧѓГіД№АИЃЎ
ЃЈ2ЃЉИљОнЬтвтСаГіЫуЪНМДПЩЧѓГіД№АИЃЎ
ЃЈ1ЃЉ![]() .
.
Д№ЃКИУМнЪЛдБдкЙЋЫОФЯБпЃЌОрРыЙЋЫО![]() .
.
ЃЈ2ЃЉЕк1ХњПЭШЫгІИЖЗбЃК![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
Ек2ХњПЭШЫгІИЖЗбЃК10дЊЃЛ
Ек3ХњПЭШЫгІИЖЗбЃК![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
Ек4ХњПЭШЫгІИЖЗбЃК10дЊЃЛ
Ек5ХњПЭШЫгІИЖЗбЃК![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
Ыљвд![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
Д№ЃКЕБЫЭЭъЕк5ХњПЭШЫЪБЃЌИУМнЪЛдБЙВЪеЕНГЕЗб68дЊ.


 КЎМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
КЎМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкШ§НЧКЏЪ§гаШчЯТЕФЙЋЪНЃК
sinЃЈІС+ІТЃЉ=sinІСcosІТ+cosІСsinІТЂй
cosЃЈІС+ІТЃЉ=cosІСcosІТЉsinІСsinІТЂк
tanЃЈІС+ІТЃЉ=![]() Ђл
Ђл
РћгУетаЉЙЋЪНПЩНЋФГаЉВЛЪЧЬиЪтНЧЕФШ§НЧКЏЪ§зЊЛЏЮЊЬиЪтНЧЕФШ§НЧКЏЪ§РДЧѓжЕЃЌШчЃК
tan105Ёу=tanЃЈ45Ёу+60ЁуЃЉ=![]() =ЉЃЈ2+
=ЉЃЈ2+![]() ЃЉЃЎ
ЃЉЃЎ
ИљОнЩЯУцЕФжЊЪЖЃЌФуПЩвдбЁдёЪЪЕБЕФЙЋЪННтОіЯТУцЕФЪЕМЪЮЪЬтЃК
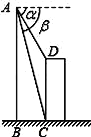
ШчЭМЃЌжБЩ§ЗЩЛњдквЛНЈжўЮяCDЩЯЗНAЕуДІВтЕУНЈжўЮяЖЅЖЫDЕуЕФИЉНЧІС=60ЁуЃЌЕзЖЫCЕуЕФИЉНЧІТ=75ЁуЃЌДЫЪБжБЩ§ЗЩЛњгыНЈжўЮяCDЕФЫЎЦНОрРыBCЮЊ42mЃЌЧѓНЈжўЮяCDЕФИпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌACЃЌBDЯрНЛгкЕуOЃЌOЪЧACЕФжаЕуЃЌAD//BCЃЌAC=8,BD=6.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєACЁЭBDЃЌЧѓЁѕABCDЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіЪЕЪ§Иљ
гаСНИіЪЕЪ§Иљ![]() .
.
(1)ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
(2)ШєЗНГЬЕФСНЪЕЪ§Иљ![]() Тњзу
Тњзу![]() ,Чѓ
,Чѓ![]() ЕФжЕЁЃ
ЕФжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє![]() ЪЧЙигк
ЪЧЙигк![]() ЕФКЏЪ§ЃЌ
ЕФКЏЪ§ЃЌ![]() ЪЧГЃЪ§ЃЈ
ЪЧГЃЪ§ЃЈ![]() ЃЉЃЌШєЖдгкДЫКЏЪ§ЭМЯѓЩЯЕФШЮвтСНЕу
ЃЉЃЌШєЖдгкДЫКЏЪ§ЭМЯѓЩЯЕФШЮвтСНЕу![]() ЃЌ
ЃЌ![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌдђГЦИУКЏЪ§ЮЊгаНчКЏЪ§ЃЌЦфжаТњзуЬѕМўЕФЫљгаГЃЪ§
ЃЌдђГЦИУКЏЪ§ЮЊгаНчКЏЪ§ЃЌЦфжаТњзуЬѕМўЕФЫљгаГЃЪ§![]() ЕФзюаЁжЕЃЌГЦЮЊИУКЏЪ§ЕФНчИп.
ЕФзюаЁжЕЃЌГЦЮЊИУКЏЪ§ЕФНчИп.
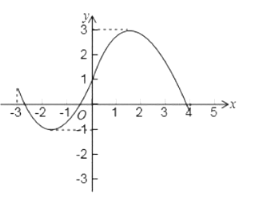
Р§ШчЃКЯТЭМЫљБэЪОЕФКЏЪ§ЕФНчИпЮЊ4.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФНчИпЃЛ
ЕФНчИпЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ЕФНчИпЮЊ4ЃЌЧѓЪЕЪ§
ЕФНчИпЮЊ4ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвбжЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФНчИпЮЊ
ЕФНчИпЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
![]()
ЃЈ1ЃЉШє![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЖШ.
ЕФГЄЖШ.
ЃЈ2ЃЉЕБЯпЖЮ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯДгзѓЯђгвЛђДггвЯђзѓдЫЖЏЪБЃЌЪдХаЖЯЯпЖЮ
ЩЯДгзѓЯђгвЛђДггвЯђзѓдЫЖЏЪБЃЌЪдХаЖЯЯпЖЮ![]() ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃЌШчЙћВЛБфЃЌЧыЧѓГіЯпЖЮ
ЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃЌШчЙћВЛБфЃЌЧыЧѓГіЯпЖЮ![]() ЕФГЄЖШЃЛШчЙћБфЛЏЃЌЧыЫЕУїРэгЩ.
ЕФГЄЖШЃЛШчЙћБфЛЏЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖЃЈ1ЃЉАрАржїШЮЖдБОАрбЇЩњНјааСЫЁАЮвзюЯВЛЖЕФПЮЭтЛюЖЏЁБЕФЕїВщЃЌВЂНЋЕїВщНсЙћЗжЮЊЪщЗЈКЭЛцЛРрМЧЮЊAЃЛвєРжРрМЧЮЊBЃЛЧђРрМЧЮЊCЃЛЦфЫћРрМЧЮЊDЃЎИљОнЕїВщНсЙћЗЂЯжИУАрУПИібЇЩњЖМНјааСЫЕШМЖЧвжЛЕЧМЧСЫвЛжжздМКзюЯВЛЖЕФПЮЭтЛюЖЏЃЎАржїШЮИљОнЕїВщЧщПіАббЇЩњЖМНјааСЫЙщРрЃЌВЂжЦзїСЫШчЯТСНЗљЭГМЦЭМЃЌЧыФуНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
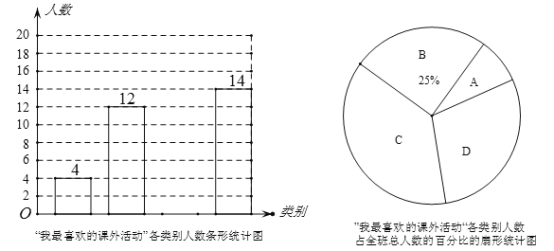
ЃЈ1ЃЉЦпФъМЖЃЈ1ЃЉАрбЇЩњзмШЫЪ§ЮЊ_______ШЫЃЌЩШаЮЭГМЦЭМжаDРрЫљЖдгІЩШаЮЕФдВаФНЧЮЊ_____ЖШЃЌЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉбЇаЃНЋОйааЪщЗЈКЭЛцЛБШШќЃЌУПАрашХЩСНУћбЇЩњВЮМгЃЌAРр4УћбЇЩњжагаСНУћбЇЩњЩУГЄЪщЗЈЃЌСэСНУћЩУГЄЛцЛЃЎАржїШЮЯжДгAРр4УћбЇЩњжаЫцЛњГщШЁСНУћбЇЩњВЮМгБШШќЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіГщЕНЕФСНУћбЇЩњЧЁКУЪЧвЛУћЩУГЄЪщЗЈЃЌСэвЛУћЩУГЄЛцЛЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШєa+bЃНabЃЌдђГЦaЁЂbЪЧЁАЯрАщЪ§ЁБЃЌР§ШчЃК3+1.5ЃН3ЁС1.5ЃЌвђДЫ3КЭ1.5ЪЧвЛзщЁАЯрАщЪ§ЁБ
ЃЈ1ЃЉЉ1гыЁЁ ЁЁЪЧвЛзщЁАЯрАщЪ§ЁБЃЛ
ЃЈ2ЃЉШєmЁЂnЪЧвЛзщЁАЯрАщЪ§ЁБЃЌ2mnЉ![]() [3m+2ЃЈ
[3m+2ЃЈ![]() nЉmЃЉ+3mnЉ6]ЕФжЕЃЎ
nЉmЃЉ+3mnЉ6]ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃЌВЂЛиД№ЮЪЬт
жгБэжадЬКЌзХгаШЄЕФЪ§бЇдЫЫуЃЌВЛгУИКЪ§вВПЩвдзїМѕЗЈЃЌР§ШчЯждкЪЧ10ЕужгЃЌ4аЁЪБвдКѓЪЧМИЕужгЃПЫфШЛ![]() ЃЌЕЋдкБэХЬЩЯПДЕНЕФЪЧ2Еужг.ШчЙћгУЗћКХЁАЈЁББэЪОжгБэЩЯЕФМгЗЈЃЌдђ
ЃЌЕЋдкБэХЬЩЯПДЕНЕФЪЧ2Еужг.ШчЙћгУЗћКХЁАЈЁББэЪОжгБэЩЯЕФМгЗЈЃЌдђ![]() .ШєЮЪ2ЕужгжЎЧА4аЁЪБЪЧМИЕужгЃЌОЭЕУЕНжгБэЩЯЕФМѕЗЈИХФюЃЌЃЌгУЗћКХЁАЁББэЪОжгБэЩЯЕФМѕЗЈ.ЃЈзЂЃКЮвУЧгУ0ЕужгДњЬц12ЕужгЃЉгЩЩЯЪіВФСЯПЩжЊЃК
.ШєЮЪ2ЕужгжЎЧА4аЁЪБЪЧМИЕужгЃЌОЭЕУЕНжгБэЩЯЕФМѕЗЈИХФюЃЌЃЌгУЗћКХЁАЁББэЪОжгБэЩЯЕФМѕЗЈ.ЃЈзЂЃКЮвУЧгУ0ЕужгДњЬц12ЕужгЃЉгЩЩЯЪіВФСЯПЩжЊЃК
ЃЈ1ЃЉ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
ЃЈ2ЃЉдкгаРэЪ§дЫЫужаЃЌЯрМгЕУСуЕФСНИіЪ§ЛЅЮЊЯрЗДЪ§ЃЌШчЙћдкжгБэдЫЫужабигУетИіИХФюЃЌдђ5ЕФЯрЗДЪ§ЪЧ______ЃЌОйР§ЫЕУїгаРэЪ§МѕЗЈЗЈдђЃКМѕШЅвЛИіЪ§ЕШгкМгЩЯетИіЪ§ЕФЯрЗДЪ§ЃЌдкжгБэдЫЫужаЪЧЗёШдШЛГЩСЂЃЛ
ЃЈ3ЃЉЙцЖЈдкжгБэдЫЫужавВга![]() ЃЌЖдгкжгБэЩЯЕФШЮвтЪ§зж
ЃЌЖдгкжгБэЩЯЕФШЮвтЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() ЪЧЗёвЛЖЈГЩСЂЃЌШєвЛЖЈГЩСЂЃЌЫЕУїРэгЩЃЛШєВЛвЛЖЈГЩСЂЃЌаДГівЛзщЗДР§ЃЌВЂНсКЯЗДР§МгвдЫЕУї.
ЪЧЗёвЛЖЈГЩСЂЃЌШєвЛЖЈГЩСЂЃЌЫЕУїРэгЩЃЛШєВЛвЛЖЈГЩСЂЃЌаДГівЛзщЗДР§ЃЌВЂНсКЯЗДР§МгвдЫЕУї.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com