
| 成绩 | 10.7 | 10.8 | 10.9 | 11.0 | 11.2 |
| 次数 | 3 | 3 | 1 | 2 | 1 |
分析 (1)根据中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);众数是一组数据中出现次数最多的数据,注意众数可以不止一个解答即可.
(2)根据平均数表示一组数据的平均程度解答即可.
解答 解:(1)运动员10次赛跑成绩的中位数是10.8秒;众数是10.8秒.若达标绩为10.8秒,则该运动员百米赛跑的达标率为$\frac{6}{10}×100%=60%$,
故答案为:10.8;10.8;60%;
(2)该名运动员10次百米赛跑的平均成绩是$\frac{10.7×3+10.8×3+10.9+11.0×2+11.2}{10}$=10.86.
点评 本题考查了平均数,中位数,众数的意义.平均水平的判断主要分析平均成绩,优秀成绩的判断从中位数不同可以得到,众数比较整体成绩.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 以上判断都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
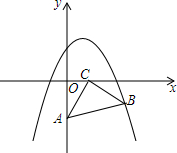 在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.
在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com