
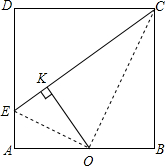
 如图,在正方形ABCD的一边上取一点E,使AE=
如图,在正方形ABCD的一边上取一点E,使AE=| 1 |
| 4 |
 解:OK2=EK•KC成立;理由如下:
解:OK2=EK•KC成立;理由如下:| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、413×106 |
| B、4.13×108 |
| C、4.13×106 |
| D、0.413×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
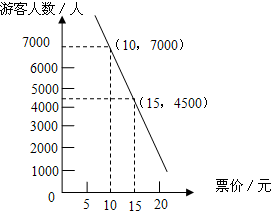 某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?
某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
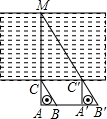 如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?
如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com