
 如图所示,在边长为2的正方形ABCD的边上有一个动点P,从点A出发沿折线ABCD移动一周后,回到A点.设点A移动的路程为x,△PAC的面积为y,求函数y的解析式.
如图所示,在边长为2的正方形ABCD的边上有一个动点P,从点A出发沿折线ABCD移动一周后,回到A点.设点A移动的路程为x,△PAC的面积为y,求函数y的解析式. 分析 要对点P所在的位置进行分类:①当点P在线段AB上移动;②当点P在线段BC上移动;③当点P在线段CD上移动;④当点P在线段DA上移动;探讨得出答案即可.
解答 解:①当点P在线段AB上移动,
即0<x≤2时,y=$\frac{1}{2}AP•BC$=x;
②当点P在线段BC上移动,
即2<x<4时,y=$\frac{1}{2}PC•AB$=$\frac{1}{2}(4-x)•2$=4-x;
③当点P在线段CD上移动,
即4<x≤6时,y=$\frac{1}{2}PC•AD$=$\frac{1}{2}(x-4)•2$=x-4;
④当点P在线段DA上移动,
即6<x<8时=0,y=$\frac{1}{2}$AP•CD=$\frac{1}{2}$(x-6)×2=x-6.
点评 本题考查动点函数问题,分段函数的应用,函数的解析式的求法,分类探讨是解决问题的关键.


科目:初中数学 来源: 题型:解答题
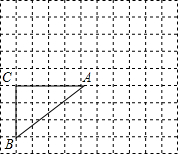 下列网格图中,每个小正方形边长均为1个单位,在Rt△ABC中,AC=4,BC=3,∠C=90°.若点B的坐标为(-3,-3),试在图中画出平面直角坐标系,根据所建立的坐标系,在给出的网格中作出与△ABC位似的△A1B1C1,使得位似中心为原点,△A1B1C1与△ABC的相似比是2,并写出A1、B1、C1点的坐标.
下列网格图中,每个小正方形边长均为1个单位,在Rt△ABC中,AC=4,BC=3,∠C=90°.若点B的坐标为(-3,-3),试在图中画出平面直角坐标系,根据所建立的坐标系,在给出的网格中作出与△ABC位似的△A1B1C1,使得位似中心为原点,△A1B1C1与△ABC的相似比是2,并写出A1、B1、C1点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
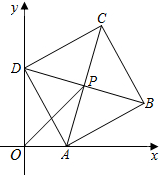 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.设点P到y轴的距离为d,则在点A,D运动的过程中,d的取值范围是2<d≤2$\sqrt{2}$.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.设点P到y轴的距离为d,则在点A,D运动的过程中,d的取值范围是2<d≤2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
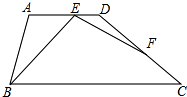 如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.
如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com