练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知$\left\{\begin{array}{l}{x+2y=5}\\{2x+y=4}\end{array}\right.$，则x+y=3．

    分析 方程组两方程相加即可求出x+y的值．

    解答 解：$\left\{\begin{array}{l}{x+2y=5①}\\{2x+y=4②}\end{array}\right.$，
    ①+②得：3（x+y）=9，
    则x+y=3．
    故答案为：3．

    点评 此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．如图所示，在边长为2的正方形ABCD的边上有一个动点P，从点A出发沿折线ABCD移动一周后，回到A点．设点A移动的路程为x，△PAC的面积为y，求函数y的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

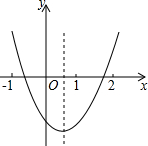    19．如图，观察二次函数y=ax2+bx+c的图象，下列结论：①a+b+c＞0，②2a+b＞0，
    ③b2-4ac＞0，④ac＞0，其中正确的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）$\sqrt{4}$+（-2008）0-（$\frac{1}{3}$）-1+|-2|
    （2）（x-y+9）（x+y-9）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．沿河岸有A，B，C三个港口，甲、乙两船同时分别从A，B港口出发，匀速驶向C港，最终到达C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．考察下列结论：
    ①甲船的速度是25km/h；
    ②从A港到C港全程为120km；
    ③甲船比乙船早1.5小时到达终点；
    ④图中P点为两者相遇的交点，P点的坐标为（$\frac{5}{6}，\frac{100}{3}$）；
    ⑤如果两船相距小于10km能够相互望见，那么，甲、乙两船可以相互望见时，x的取值范围是$\frac{2}{3}$＜x＜2．
    其中正确的结论有②．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

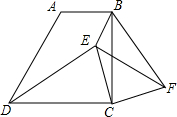    13．在梯形ABCD中AB∥CD，∠BCD=90°，AB=1，BC=2，tan∠ADC=2．
    （1）求证：BC=CD；
    （2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△EFC的形状，并证明；
    （3）在（2）的条件下，当BE：CE=1：2，∠BEC=135°时，求sin∠BFE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，AO⊥CO，BO⊥DO，∠AOD=150°，则∠BOC的度数是30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\frac{{\sqrt{2}}}{2}$sin45°-$\sqrt{12}$sin60°-2tan45°；    
    （2）$\frac{{2{sin}{{30}°}}}{{2{sin}{{60}°}-tan{4}{{5}°}}}-\frac{3}{2}cos{60°}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．若y=$\sqrt{x-5}+\sqrt{15-3x}-3$，则x-y=8．

    查看答案和解析>>

    同步练习册答案