
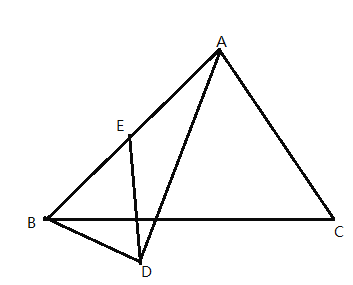
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的平分线上一点,
的平分线上一点,![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
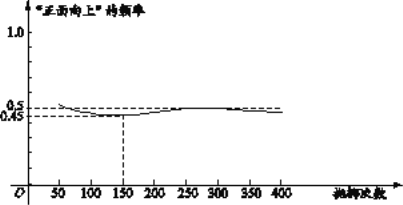
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
已知点D为等边△ABC 的边AB所在直线上一动点(点D与点A和点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接 AE.
操作发现:
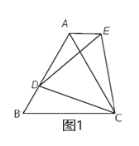
(1)如图1,点D在边AB上,则 AE与BD 有怎样的数量关系? 说明理由;
类比猜想:
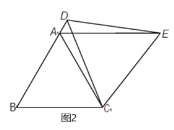
(2)如图2,若点D在边BA延长线上,则 AE与BD有怎样的数量关系? 说明理由;
拓广探究:
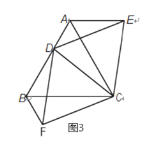
(3)如图3,点D在边AB上,以CD为边分别在CD下方和上方作等边△CDF 和等边△CDE,连接 AE,BF,直接写出AE,BF与 AB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
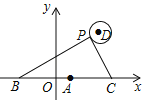
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
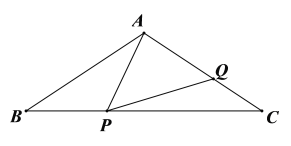
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点P从点B出发,以
,点P从点B出发,以![]() 速度沿
速度沿![]() 向点C运动,设点P的运动时间为t秒.
向点C运动,设点P的运动时间为t秒.
(1)![]() _______
_______![]() .(用含t的代数式表示)
.(用含t的代数式表示)
(2)当点P从点B开始运动,同时,点Q从点C出发,以![]() 的速度沿
的速度沿![]() 向点A运动,当
向点A运动,当![]() ≌
≌![]() 时,求v的值.
时,求v的值.
(3)在(2)的条件下,求![]() ≌
≌![]() 时v的值.
时v的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com