
【题目】关于二次函数![]() 的三个结论:①对任意实数m,都有
的三个结论:①对任意实数m,都有![]() 与
与![]() 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则![]() 或
或![]() ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则![]() 或
或![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.①③C.②③D.①②③
【答案】D
【解析】
由题意可求次函数y=ax2-4ax-5的对称轴为直线![]() ,由对称性可判断①;分a>0或a<0两种情况讨论,由题意列出不等式,可求解,可判断②;分a>0或a<0两种情况讨论,由题意列出不等式组,可求解,可判断③;即可求解.
,由对称性可判断①;分a>0或a<0两种情况讨论,由题意列出不等式,可求解,可判断②;分a>0或a<0两种情况讨论,由题意列出不等式组,可求解,可判断③;即可求解.
解:∵抛物线的对称轴为![]() ,
,
∴x1=2+m与x2=2-m关于直线x=2对称,
∴对任意实数m,都有x1=2+m与x2=2-m对应的函数值相等;
故①正确;
当x=3时,y=-3a-5,当x=4时,y=-5,
若a>0时,当3≤x≤4时,-3a-5<y≤-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴![]() ,
,
若a<0时,当3≤x≤4时,-5≤y<-3a-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴![]() ,
,
故②正确;
若a>0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≥0,
∴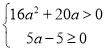 ,
,
∴![]() ;
;
若a<0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≤0,
∴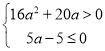
∴a<![]() ,
,
综上所述:当a<![]() 或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
故③正确;
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
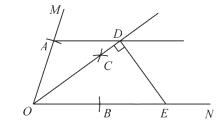
【题目】如图,已知![]() 是一个锐角,以点
是一个锐角,以点![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,画射线
,画射线![]() .过点
.过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设
.设![]() ,
,![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
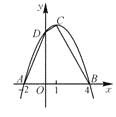
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
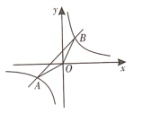
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且
的图象交于A,B两点,若点P是第一象限内反比例函数图象上一点,且![]() 的面积是
的面积是![]() 的面积的2倍,则点P的横坐标为________.
的面积的2倍,则点P的横坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到加工粮食任务,要求![]() 天加工完
天加工完![]() 吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量
吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图①所示;未加工粮食
(天)之间的函数关系如图①所示;未加工粮食![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图②所示、请结合图象解答下列问题:
(天)之间的函数关系如图②所示、请结合图象解答下列问题: ![]()
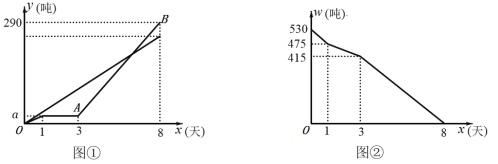
(1)甲车间每天加工粮食 吨,![]() ;
;
(2)求乙车间维修设备后,乙车间加工粮食数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求加工![]() 吨粮食需要几天完成.
吨粮食需要几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
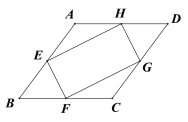
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
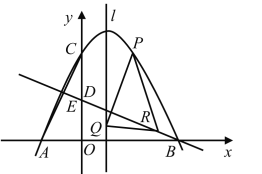
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com