
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
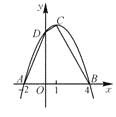
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
【答案】(1)、y=-![]() +2x+8;(2)、30.
+2x+8;(2)、30.
【解析】
试题根据交点和最值得出顶点坐标,然后将解析式设成顶点式,然后将交点代入求出a的值;将四边形的面积转化成△AOD的面积+四边形DOEC的面积+△BCE的面积进行求解.
试题解析:(1)由抛物线的对称性知,它的对称轴是x=1. 又∵函数的最大值为9,
∴抛物线的顶点为C(1,9). 设抛物线的解析式为y=a![]() +9,代入B(4,0),求得a=-1.
+9,代入B(4,0),求得a=-1.
∴二次函数的解析式是y=-![]() +9, 即y=-
+9, 即y=-![]() +2x+8.
+2x+8.
(2)
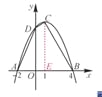
当x=0时,y=8,即抛物线与y轴的交点坐标为D(0,8).
过C作CE⊥x轴于E点.
∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE=![]() ×2×8+
×2×8+![]() ×(8+9)×1+
×(8+9)×1+![]() ×3×9=30.
×3×9=30.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
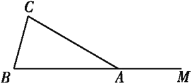
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
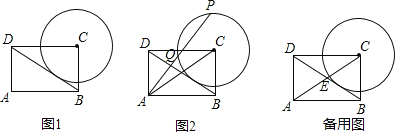
【题目】已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切.
(1)如图1,求⊙C的半径;
(2)如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC=![]() ,求∠CPA的度数和弧PQ的长;
,求∠CPA的度数和弧PQ的长;
(3)如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤![]() 时,请直接写出∠PCE度数的取值范围.
时,请直接写出∠PCE度数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园音乐之声“结束后,王老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如下频数直方图和扇形统计图:
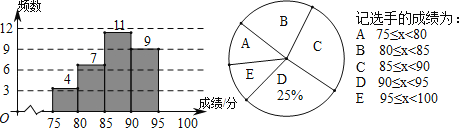
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形E的圆心角度数;
(3)成绩在E区域的选手中,男生比女生多一人,从中随机选取两人,求恰好选中两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
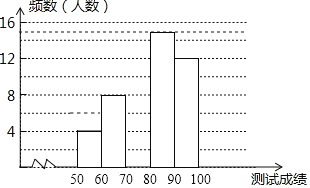
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2018年1月的利润为200万元.设2018年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2018年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
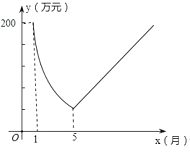
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间对应的函数关系式.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2018年1月的水平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,点G在边
,点G在边![]() 上,连接
上,连接![]() ,作
,作![]() 于点E,
于点E,![]() 于点F,连接
于点F,连接![]() 、
、![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
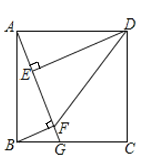
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若点G从点B沿![]() 边运动至点C停止,求点E,F所经过的路径与边
边运动至点C停止,求点E,F所经过的路径与边![]() 围成的图形的面积.
围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() 的三个结论:①对任意实数m,都有
的三个结论:①对任意实数m,都有![]() 与
与![]() 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则![]() 或
或![]() ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则![]() 或
或![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平而直角坐标系中,已知点![]() ,直线
,直线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 恰好经过
恰好经过![]() 三点中的两点.
三点中的两点.
![]() 判断点
判断点![]() 是否在直线
是否在直线![]() 上.并说明理由;
上.并说明理由;
![]() 求
求![]() 的值;
的值;
![]() 平移抛物线
平移抛物线![]() ,使其顶点仍在直线
,使其顶点仍在直线![]() 上,求平移后所得抛物线与
上,求平移后所得抛物线与![]() 轴交点纵坐标的最大值.
轴交点纵坐标的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com