
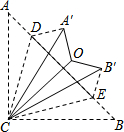
 如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
分析 如图所示,延长CO到F,由翻折的性质可知:∠A′CF=$\frac{1}{3}∠ACF$,$∠B′CF=\frac{1}{3}∠BCF$,∠CA′O=∠DA′O=∠A=45°,∠OB′C=∠CB′E=∠ECB=45°,最后利用三角形外角的性质可求得∠A′OB′的度数.
解答 解:如图所示:延长CO到F.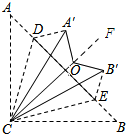
∵AB=BC,∠ACB=90°,
∴∠A=∠B=45°.
由翻折的性质可知:∠A′CF=$\frac{1}{3}∠ACF$,$∠B′CF=\frac{1}{3}∠BCF$,∠CA′O=∠DA′O=∠A=45°,∠OB′C=∠CB′E=∠ECB=45°.
∴∠A′CB′=∠A′CF+∠B′CF=$\frac{1}{3}∠ACB$=30°.
∴∠A′OB′=∠A′CB′+∠CA′O+∠OB′C=30°+45°+45°=120°.
故选:B.
点评 本题主要考查的是翻折的性质,利用翻折的性质求得∠A′CB′=30°,∠CA′O=45°,∠OB′C=45°是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
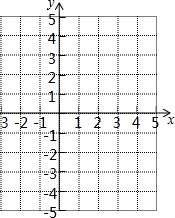 已知在平面直角坐标系中点A(-2,-2),B(1,-2),C(3,2),D(0,2)按照下列要求作图:
已知在平面直角坐标系中点A(-2,-2),B(1,-2),C(3,2),D(0,2)按照下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小强今年12岁,明年百分之二百地是13岁 | |
| B. | 同时抛掷两枚硬币,同是正面或同是反面朝上的可能性比一正一反大 | |
| C. | 两个不透明的布袋中都放有除颜色外完全相同的球,甲布袋有6个红球,乙布袋中有8个红球,那么在甲、乙两布袋中各任意摸一球,从乙布袋中摸到红球的概率大 | |
| D. | 盒子里装有10个完全相同的纸团,只有一个纸团内写有“奖”,而另九个纸团内均为“谢谢惠顾”,10名参与者可从中任摸一个纸团,则先摸的和后摸的“中奖”概率一样大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com