
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N. | m |
| x |
|
| m |
| x |
| 1 |
| 2 |
|
|
| 1 |
| 4 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| x |
| 4 |
| x |
| 1 |
| 2 |
| 4 |
| x |
| 4 |
| x |


科目:初中数学 来源: 题型:
| 8 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
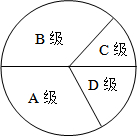 为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:| 等级 | A级 (≥90分) |
B级 (≥70分且<90分) |
C级 (≥60分且<70分) |
D级 (<60分) |
| 人数 | 22 | 28 | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
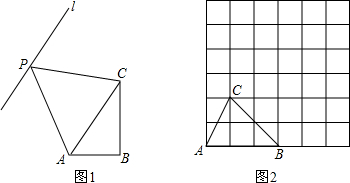
查看答案和解析>>
科目:初中数学 来源: 题型:
| 价格 类型 |
进价(元/件) | 售价(元/件) |
| 甲 | 300 | 380 |
| 乙 | 500 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:
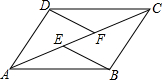 已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com