
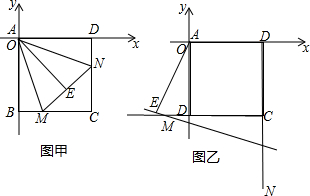
分析 (1)证得Rt△AEN≌Rt△ADN,Rt△ABM≌△AEN,得出∠EAN=∠DAN,∠BAM=∠EAM,EN=DN,ME=BM,得出∠MAN=45°,△MCN的周长=4;
(2)连接AM,证Rt△AEM≌Rt△ABM,连接AN,证Rt△AEN≌Rt△ADN,从而得DN=BM+MN;
(3)设出CN=m,利用(1)中的条件表示出CM,MN,进一步利用勾股定理求得m,进一步利用三角形的面积计算公式求得答案即可.
解答 解:(1)∠MAN=45°,△MCN的周长=4;
(2)如图,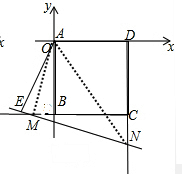
连接AM,
在Rt△AEM和Rt△ABM中,
$\left\{\begin{array}{l}{AE=AD}\\{AM=AM}\end{array}\right.$,
∴Rt△AEM≌Rt△ABM,
∴EM=BM,
在Rt△AEN和Rt△ADN中,
$\left\{\begin{array}{l}{AE=AD}\\{AN=AN}\end{array}\right.$,
∴Rt△AEN≌Rt△ADN,
∴DN=NE=MN+ME=MN+BM,
即DN=BM+MN.
③∵Rt△AEN≌Rt△ADN,Rt△ABM≌△AEN,
∴EN=DN,ME=BM,
设BM=x,CN=m,
则MC=2-x,DN=2-m,
∴MN=2+x-m,
在Rt△CMN中,
(2-x)2+m2=(2+x-m)2,
解得:m=$\frac{4x}{x+2}$,
S△MCN=$\frac{1}{2}$CM•CN=$\frac{1}{2}$(2-x)•$\frac{4x}{x+2}$=$\frac{4x(2-x)}{x+2}$,
即S=$\frac{1}{2}$CM•CN=$\frac{4x(2-x)}{x+2}$.
点评 此题考查四边形的综合题,综合考查了正方形的性质,三角形全等的判定与性质,勾股定理以及三角形的面积计算,正确做出辅助线,掌握三角形全等的判定方法是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码(cm) | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 1 | 1 | 2 | 4 | 2 |
| A. | 4cm,26cm | B. | 4cm,26.5cm | C. | 26.5cm,26.5cm | D. | 26.5cm,26cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
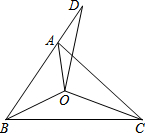 如图,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO,若BD=BC,∠ABC=54°,则∠BCA的度数为42°.
如图,已知△ABC三个内角的平分线交于点O,延长BA到点D,使AD=AO,连接DO,若BD=BC,∠ABC=54°,则∠BCA的度数为42°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
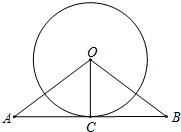 如图,在等腰△OAB中,OA=OB,以点O为圆心,作圆与底边AB相切于点C.
如图,在等腰△OAB中,OA=OB,以点O为圆心,作圆与底边AB相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
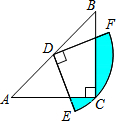 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com