
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
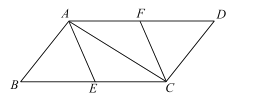
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
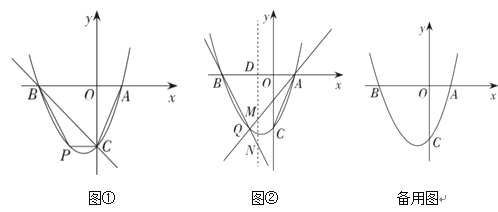
【题目】如图①,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的函数解析式;
(2)如图①,点![]() 在第三象限内的抛物线上.
在第三象限内的抛物线上.
①连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
②![]() 为
为![]() 轴上一点,当
轴上一点,当![]() 取得最小值时,求点
取得最小值时,求点![]() 的坐标;
的坐标;
(3)如图②,![]() 为
为![]() 轴下方抛物线上任意一点,
轴下方抛物线上任意一点,![]() 是抛物线的对称轴与
是抛物线的对称轴与![]() 轴的交点,直线
轴的交点,直线![]() ,
,![]() 分别交抛物线的对称轴于点
分别交抛物线的对称轴于点![]() ,
,![]() .问:
.问:![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 点在边
点在边![]() 上,连接
上,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,且
,且![]() 与四边形
与四边形![]() 的周长相等,设
的周长相等,设![]() ,
,![]() .
.
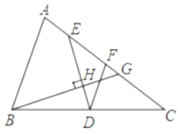
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一道满分3分的数学测验题,网络阅卷时老师评分只能给整数,即得分可能为0分,1分,2分,3分.为了解学生知识点掌握情况及试题的难易程度,对初三(1)班所有学生的这道试题得分情况进行分析整理后,绘制了两幅尚不完整的统计图,如图所示.
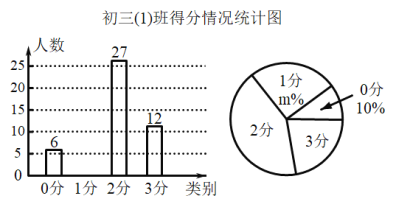

根据以上信息,解答下列问题:
(1)m= ,得分为“3分”对应的扇形圆心角为 度,请补全条形统计图;
(2)由“小知识”提供的信息,请依据计算得到的L的值,判断这道题属于哪一类难度的试题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.在不改变矩形ABCD的形状和大小的情况下,当矩形的顶点A在x轴的正半轴上左右移动时,另一个顶点D始终在y轴的正半轴上随之上下移动.
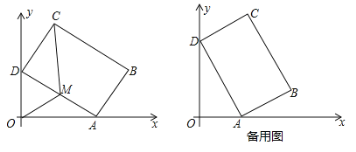
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,若四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)在点A移动过程中是否存在某一位置,使点C到点O的距离有最大值?若存在,求此时的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地向湖北派遣由5名医护人员组成的一支医疗队,支援抗击新型冠状病毒肺炎疫情.已知这五名医护人员的年龄分别为24,28,36,36,47(单位:岁),其中年龄为24,47岁的是女队员,其余是男队员.
(1)求这五名医护人员的年龄的众数;
(2)若因疫情需要,需增加一名医护人员,若增加后年龄的中位数小于原来年龄的中位数,则增加医护人员的最大年龄是多少?
(3)若需要从男性队员中选两名参加重症病人抢救,求所选两名队员的年龄恰好相等的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其他垃圾. 现有甲、乙二人,其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率.
(2)用画树状图或列表的方法求乙所拿的垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 边的中点.将
边的中点.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
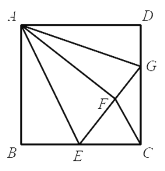
A.①②B.①③④C.②③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com