
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
【答案】(1)今年每套![]() 型的价格各是1.2万元、
型的价格各是1.2万元、![]() 型一体机的价格是1.8万元;(2)该市明年至少需投入1800万元才能完成采购计划.
型一体机的价格是1.8万元;(2)该市明年至少需投入1800万元才能完成采购计划.
【解析】
(1)直接利用今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机,分别得出方程求出答案;
型一体机,分别得出方程求出答案;
(2)根据题意表示出总费用进而利用一次函数增减性得出答案.
(1)设今年每套![]() 型一体机的价格为
型一体机的价格为![]() 万元,每套
万元,每套![]() 型一体机的价格为
型一体机的价格为![]() 万元,
万元,
由题意可得:![]() ,
,
解得:![]() ,
,
答:今年每套![]() 型的价格各是1.2万元、
型的价格各是1.2万元、![]() 型一体机的价格是1.8万元;
型一体机的价格是1.8万元;
(2)设该市明年购买![]() 型一体机
型一体机![]() 套,则购买
套,则购买![]() 型一体机
型一体机![]() 套,
套,
由题意可得:![]() ,
,
解得:![]() ,
,
设明年需投入![]() 万元,
万元,
![]()
![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
故该市明年至少需投入1800万元才能完成采购计划.


科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售![]() 型和
型和![]() 型两种学习机,其中用10000元采购
型两种学习机,其中用10000元采购![]() 型学习机台数和用8000元采购
型学习机台数和用8000元采购![]() 型学习机台数相等,且一台
型学习机台数相等,且一台![]() 型学习机比一台
型学习机比一台![]() 型学习机进价多100元.
型学习机进价多100元.
(1)求一台![]() 型和
型和![]() 型学习机价格各是多少元?
型学习机价格各是多少元?
(2)若购进![]() 型学习机共100台,其中
型学习机共100台,其中![]() 型的进货量不超过
型的进货量不超过![]() 型的2倍,设购进
型的2倍,设购进![]() 型学习机
型学习机![]() 台.
台.
①求![]() 的取值范围.
的取值范围.
②已知![]() 型学习机售价均是900元/台,实际进货时,厂家对
型学习机售价均是900元/台,实际进货时,厂家对![]() 型学习机在原进货价的基础,上下调
型学习机在原进货价的基础,上下调![]() 元,且限定商店最多购进
元,且限定商店最多购进![]() 型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润
型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
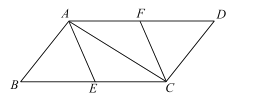
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一段时期内对某种商品经销情况进行统计得到该商品的销售数量![]() (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价
(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价![]() (元/件,
(元/件,![]() )成反比例,销售过程中得到的部分数据如下:
)成反比例,销售过程中得到的部分数据如下:
售价 | 8 | 10 |
销售数量 | 70 | 58 |
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
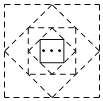
【题目】如图,小聪用一张面积为1的正方形纸片,按如下方式操作:
①将正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,把四个等腰直角三角形扔掉;
②在余下纸片上依次重复以上操作,
当完成第2020次操作时,余下纸片的面积为( )
A.22019B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
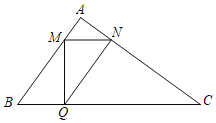
【题目】如图,在ABC中,∠A=90°,AB=3,AC=4,点M、Q分别是边AB、BC上的动点(点M不与A、B重合),且MQ⊥BC,过点M作MN∥BC.交AC于点N,连接NQ,设BQ=x.
(1)是否存在一点Q,使得四边形BMNQ为平行四边形,并说明理由;
(2)当BM=2时,求x的值;
(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
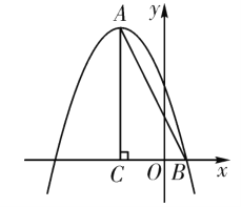
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,使
,使![]() .
.
①求点![]() 的坐标和
的坐标和![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,直接写出符合条件的所有点
为直角三角形?若存在,直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,点
,点![]() 关于线段
关于线段![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,连接
上的一个动点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 的值最小时,则
的值最小时,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com