
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 点在边
点在边![]() 上,连接
上,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,且
,且![]() 与四边形
与四边形![]() 的周长相等,设
的周长相等,设![]() ,
,![]() .
.
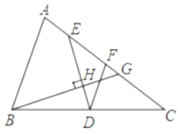
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据中位线的性质和定义得DF =![]() c,CF=
c,CF=![]() b,结合△CDE与四边形ABDE的周长相等,得到CE=
b,结合△CDE与四边形ABDE的周长相等,得到CE=![]() ,可得EF的长,进而即可得到结论;
,可得EF的长,进而即可得到结论;
(2)连接BE,DG,过点A作AP⊥BG于P,过B作BM⊥DG于M,过E作EN⊥DG于N,证明四边形BMNE是平行四边形,易得BE∥DG,从而得到△ABE∽△FDG,进而得到FG=![]() (bc),再证∠BAP=∠DEF=∠PAC,得到△ABP≌△AGP,从而得AB=AG=c,结合CF=FG+CG,得到关于b,c的等式,即可得到结论.
(bc),再证∠BAP=∠DEF=∠PAC,得到△ABP≌△AGP,从而得AB=AG=c,结合CF=FG+CG,得到关于b,c的等式,即可得到结论.
(1)证明:∵点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() .
.
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∵![]() 与四边形
与四边形![]() 的周长相等,
的周长相等,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过B作BM⊥DG于M,过E作EN⊥DG于N,如图所示.
,过B作BM⊥DG于M,过E作EN⊥DG于N,如图所示.

∵![]() ,
,
∴![]()
∴![]() ,
,
∵△BDG和△EDG的底边为DG,
∴底边DG上的高BM=EN.
∵BM⊥DG,EN⊥DG,
∴BM∥EN,
∴四边形BMNE是平行四边形,
∴BE∥DG.
∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∴∠BAE=∠DFG.
∵BE∥DG,
∴∠AEB=∠FGD,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠BAE=∠DFG=2∠DEF,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴∠APB=∠APG=90°.
∵AP=AP,
∴△ABP≌△AGP,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
(1)求点D的坐标和直线BC对应的一次函数关系式;
(2)若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;
(3)如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.
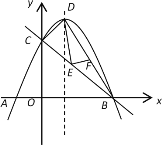
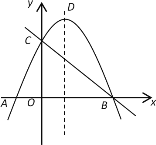
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=x-1交x轴、y轴于A、B点,点P(1,![]() ,且S四边形PAOB=3.5,双曲线y=
,且S四边形PAOB=3.5,双曲线y=![]() 经过点P.
经过点P.
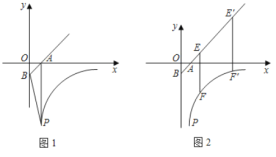
(1)求k的值;
(2)如图2,直线![]() )交射线BA于E,交双曲线y=
)交射线BA于E,交双曲线y=![]() 于F,将直线
于F,将直线![]() 向右平移4个单位长度后交射线于
向右平移4个单位长度后交射线于![]() ,交双曲线y=
,交双曲线y=![]() 于
于![]() ,若
,若![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
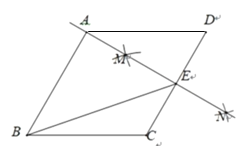
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
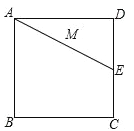
【题目】如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
A.![]() cm或
cm或![]() cm B.
cm B.![]() cm C.
cm C.![]() cm或
cm或![]() cm D.
cm D.![]() cm或
cm或![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售![]() 型和
型和![]() 型两种学习机,其中用10000元采购
型两种学习机,其中用10000元采购![]() 型学习机台数和用8000元采购
型学习机台数和用8000元采购![]() 型学习机台数相等,且一台
型学习机台数相等,且一台![]() 型学习机比一台
型学习机比一台![]() 型学习机进价多100元.
型学习机进价多100元.
(1)求一台![]() 型和
型和![]() 型学习机价格各是多少元?
型学习机价格各是多少元?
(2)若购进![]() 型学习机共100台,其中
型学习机共100台,其中![]() 型的进货量不超过
型的进货量不超过![]() 型的2倍,设购进
型的2倍,设购进![]() 型学习机
型学习机![]() 台.
台.
①求![]() 的取值范围.
的取值范围.
②已知![]() 型学习机售价均是900元/台,实际进货时,厂家对
型学习机售价均是900元/台,实际进货时,厂家对![]() 型学习机在原进货价的基础,上下调
型学习机在原进货价的基础,上下调![]() 元,且限定商店最多购进
元,且限定商店最多购进![]() 型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润
型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
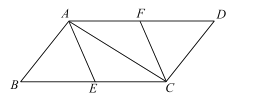
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
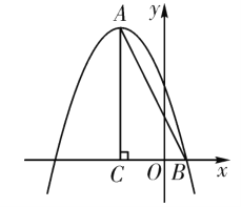
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,使
,使![]() .
.
①求点![]() 的坐标和
的坐标和![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,直接写出符合条件的所有点
为直角三角形?若存在,直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com