
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() 经过点
经过点![]() 过点
过点![]() 作
作![]() 的切线
的切线![]() 点
点![]() 是
是![]() 上不与点
上不与点![]() 重合的一个动点,连接
重合的一个动点,连接![]() .
.
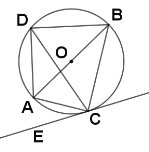
![]() 求证:
求证:![]() ;
;
![]() 填空:
填空:
![]() 当
当![]() _ 时,
_ 时,![]() 为等腰直角三角形:
为等腰直角三角形:
![]() 当
当![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
【答案】![]() 见解析;
见解析;![]() ①45°②120°
①45°②120°
【解析】
(1)连接OC.根据等腰三角形的性质得到∠OCB=∠OBC,根据平行线的性质得到∠ACB=90°.再根据切线的性质定理及圆周角定理即可得到结论;
(2)①根据圆的对称性由BD=AD可得弧BD=弧AD,再由圆周角定理得∠DCB=∠DCA,进而得解;
②由菱形可得OD=AD,结合OD=OA,证得△OAD为等边三角形,则∠OAD=60°,最后根据圆周角定理即可得解.
解:![]() 如图,连接
如图,连接![]()
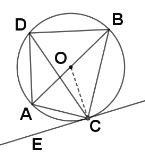
![]()
![]()
![]() 为
为![]() 的直径,
的直径,
![]()
![]() ,
,
![]() 是
是![]() 的切线,
的切线,
![]()
![]()
![]()
![]()
![]()
(2)①∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴AD=DB,
∴弧AD=弧DB,
∴∠ACD=∠DCB=![]() ∠ACB,
∠ACB,
∵∠ACB=90°,
∴∠DCB=45°,
②∵四边形![]() 为菱形,
为菱形,
∴OD=AD,
又∵OD=OA,
∴OD=OA=AD,
∴△AOD为等边三角形,
∴∠OAD=60°,
∵∠OAD=![]() ∠DOB,
∠DOB,
∴∠DOB=120°.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
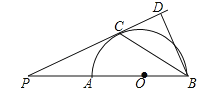
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠C=90°,AC=2,BC=2![]() ,点O是边AB上的一个动点,以点O为圆心,OA为半径作⊙O,与边AC交于点M.
,点O是边AB上的一个动点,以点O为圆心,OA为半径作⊙O,与边AC交于点M.
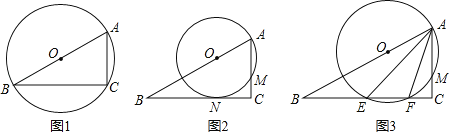
(1)如图1,当⊙O经过点C时,⊙O的直径是 ;
(2)如图2,当⊙O与边BC相切时,切点为点N,试求⊙O与△ABC重合部分的面积;
(3)如图3,当⊙O与边BC相交时,交点为E、F,设CM=x,就判断AEAF是否为定值,若是,求出这个定值;若不是,请用含x的代数式表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
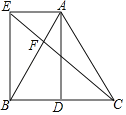
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小字计划在某外卖网站点如下表所示的菜品,已知每份订单的配送费为3元,商家为了促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元,如果小宇在购买下表中所有菜品时,采取适当的下订单方式,那么他点餐的总费用最低可为___元.
菜品 | 单价(含包装费) | 数量 |
| 30元 | 1 |
| 12元 | 1 |
| 30元 | 1 |
| 12元 | 1 |
| 3元 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用家用燃气灶烧开同一壶水所需的燃气量![]() (单位:
(单位:![]() )与旋钮的旋转角度
)与旋钮的旋转角度![]() (单位:度)(
(单位:度)(![]() )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度
)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度![]() 与燃气量
与燃气量![]() 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,以点
,以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径画弧,与直线
的长为半径画弧,与直线![]() 位于第一象限的部分相交于点
位于第一象限的部分相交于点![]() ,则点
,则点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,反比例函数![]() (k是常数,且
(k是常数,且![]() )的图象经过点
)的图象经过点![]() .
.
(1)若b=4,求y关于x的函数表达式;
(2)点![]() 也在反比例函数y的图象上:
也在反比例函数y的图象上:
①当![]() 且
且![]() 时,求b的取值范围;
时,求b的取值范围;
②若B在第二象限,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com