
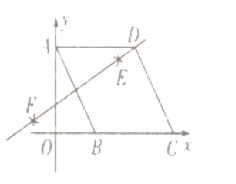
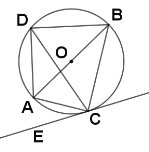
【题目】如图,在菱形![]() 中,点
中,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() 分别以点
分别以点![]() 为圆心、大于
为圆心、大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() .直线
.直线![]() 恰好经过点
恰好经过点![]() 则点
则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
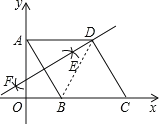
连接DB,如图,利用基本作图得到EF垂直平分AB,则DA=DB,再根据菱形的性质得到AD∥BC,AD=AB,则可判断△ADB为等边三角形,所以∠DAB=∠ABO=60°,然后计算出OB=2,从而得到B点坐标.
解:连接DB,如图,
由作法得EF垂直平分AB,
∴DA=DB,
∵四边形ABCD是菱形,
∴AD∥BC,AD=AB,
∴AD=AB=DB,
∴△ADB为等边三角形,
∴∠DAB=60°,
∴∠ABO=60°,
∵A(0,![]() ),
),
∴OA=![]() ,
,
∵∠ABO=60°,∠AOB=90°,
∴∠BAO=30°,
∴在Rt△AOB中,AB=2OB,
∵OB2+OA2=AB2,
∴OB2+![]() 2=(2OB)2,
2=(2OB)2,
∴OB=2(舍负),
∴B(2,0).
故选:C.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
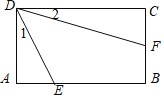
【题目】如图,矩形ABCD长与宽的比为3:2,点E,F分别在边AB、BC上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)=( )
,则cos(∠1+∠2)=( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桃花中学计划购买![]() 两种型号的小黑板,经洽谈, 购买一块
两种型号的小黑板,经洽谈, 购买一块![]() 型小黑板比买一块
型小黑板比买一块![]() 型小黑板多
型小黑板多![]() 元,且购买
元,且购买![]() 块
块![]() 型小黑板和
型小黑板和![]() 块
块![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求购买一块![]() 型小黑板和一块
型小黑板和一块![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根据学校的实际情况,需购买![]() 两种型号的小黑板共
两种型号的小黑板共![]() 块,并且购买
块,并且购买![]() 型小黑板的数量不少于购买
型小黑板的数量不少于购买![]() 型小黑板的数量,请问学校购买这批小黑板最少要多少元?
型小黑板的数量,请问学校购买这批小黑板最少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会已于2019年4月29日在北京市延庆区开展,吸引了大批游客参观游览.五一小长假期间平均每天入园人数大约是8万人,佳佳等5名同学组成的学习小组,随机调查了五一假期中入园参观的部分游客,获得了他们在园内参观所用时间,并对数据进行整理,描述和分析,下面给出了部分信息:
a.参观时间的频数分布表如下:
时间 | 频数(人数) | 频率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合计 |
| 1.000 |
b.参观时间的频数分布直方图如图:
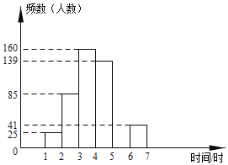
根据以上图表提供的信息,解答下列问题:
(1)这里采用的调查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并请补全频数分布直方图;
(4)请你估算五一假期中平均每天参观时间小于4小时的游客约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() 经过点
经过点![]() 过点
过点![]() 作
作![]() 的切线
的切线![]() 点
点![]() 是
是![]() 上不与点
上不与点![]() 重合的一个动点,连接
重合的一个动点,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 填空:
填空:
![]() 当
当![]() _ 时,
_ 时,![]() 为等腰直角三角形:
为等腰直角三角形:
![]() 当
当![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 和
和![]() 是一次函数
是一次函数![]() 与反比例函数
与反比例函数![]() 图象的两个不同交点,点
图象的两个不同交点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 以及
以及![]() 分别与
分别与![]() 轴交与点
轴交与点![]() 和点
和点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有M、N两点,M点表示的数分别为m,N点表示的数是n(n>m),则线段MN的长(点M到点N的距离)可表示为MN=n﹣m,请用上面材料中的知识解答下面的问题:一个点从数轴上的原点O开始,先向左移动3cm到达A点,再向右移动2cm到达B点,然后向右移动4cm到达C点,用1cm表示1个单位长度.
(1)请你在数轴上表示出A、B、C三点的位置,并直接写出线段AC的长度.
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点所表示的数.
(4)若点P以从点A向原点O移动,同时点Q以与点P相同的速度从原点O向点C移动,试探索:PQ的长是否会发生改变?如果不变,请求出PQ的长.如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数![]() (a,b,c是常数)时,甲发现当x=-1时函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
(a,b,c是常数)时,甲发现当x=-1时函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com