
【题目】已知:△ABC内接于⊙O,过点A作直线EF.
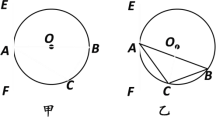
(1)如图甲,AB为直径,要使EF为⊙O的切线,还需添加的条件是(写出两种情况,不需要证明):① 或② ;
(2)如图乙,AB是非直径的弦,若∠CAF=∠B,求证:EF是⊙O的切线.
(3)如图乙,若EF是⊙O的切线,CA平分∠BAF,求证:OC⊥AB.
【答案】(1)①OA⊥EF;②∠FAC=∠B;(2)见解析;(3)见解析.
【解析】
(1) 添加条件是:①OA⊥EF或∠FAC=∠B根据切线的判定和圆周角定理推出即可.
(2) 作直径AM,连接CM,推出∠M=∠B=∠EAC,求出∠FAC+∠CAM=90°,根据切线的判定推出即可.
(3)由同圆的半径相等得到OA=OB,所以点O在AB的垂直平分线上,根据∠FAC=∠B,∠
BAC=∠FAC,等量代换得到∠BAC=∠B,所以点C在AB的垂直平分线上,得到OC垂直平分AB.
(1)①OA⊥EF②∠FAC=∠B,
理由是:①∵OA⊥EF,OA是半径,
∴EF是⊙O切线,
②∵AB是⊙0直径,
∴∠C=90°,
∴∠B+∠BAC=90°,
∵∠FAC=∠B,
∴∠BAC+∠FAC=90°,
∴OA⊥EF,
∵OA是半径,
∴EF是⊙O切线,
故答案为:OA⊥EF或∠FAC=∠B,
(2)作直径AM,连接CM,
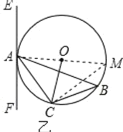
即∠B=∠M(在同圆或等圆中,同弧所对的圆周角相等),
∵∠FAC=∠B,
∴∠FAC=∠M,
∵AM是⊙O的直径,
∴∠ACM=90°,
∴∠CAM+∠M=90°,
∴∠FAC+∠CAM=90°,
∴EF⊥AM,
∵OA是半径,
∴EF是⊙O的切线.
(3)∵OA=OB,
∴点O在AB的垂直平分线上,
∵∠FAC=∠B,∠BAC=∠FAC,
∴∠BAC=∠B,
∴点C在AB的垂直平分线上,
∴OC垂直平分AB,
∴OC⊥AB.


科目:初中数学 来源: 题型:
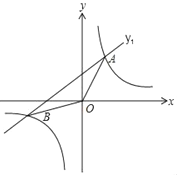
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(2,4),B(﹣4,m)两点.
与一次函数y2=k2x+b的图象交于点A(2,4),B(﹣4,m)两点.
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() ≥k2x+b的解.
≥k2x+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
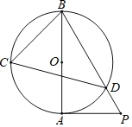
【题目】如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ取最小值时,Q点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“传统文化”知识竞赛,已知该校七年级男生和女生各有学生200人,从中各随机抽取20名学生进行抽样调查,获得了他们知识竞赛成绩(满分100分),并进行整理,得到下面部分信息.
男生:74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
女生:76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91
成绩 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
男生 | 0 | 1 | 10 | 1 | 8 |
女生 | 1 | 2 | a | 8 | 6 |
平均数、中位数、众数、方差如表所示:
成绩 | 平均数 | 中位数 | 众数 | 方差 |
男生 | 84 | 77 | 74 | 145.4 |
女生 | 84 | b | 89 | 115.6 |
根据以上信息,回答下列问题:
(1)a= ,b= ;
(2)你认为七年级学生中,男生还是女生的总体成绩较好,为什么?(至少从两个不同的角度说明)
(3)若在此次竞赛中,该校七年级学生中有四人取得100分的好成绩,且恰好是两个男生两个女生.现从这四人中随机抽取两人参加市里的竞赛,求这两人恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com