
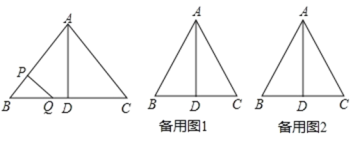
����Ŀ����ͼ,��ABC��,AB=AC=10����,BC=12����,D��BC���е�,��P��B����,��a����/��(a>0)���ٶ���BA�������A�˶�����Qͬʱ��1����/����ٶȴ�D��������DB�������B�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶��������ǵ��˶�ʱ��Ϊt�롣
(1)��a=![]() ��t=2,��֤����ABC�ס�PBQ��2����a=2����ôtΪ��ֵʱ���� B��P��QΪ���������������ABD����?˵�����ɡ�
��t=2,��֤����ABC�ס�PBQ��2����a=2����ôtΪ��ֵʱ���� B��P��QΪ���������������ABD����?˵�����ɡ�
���𰸡�(1)������;(2)������.
��������
��1���������⽫PB��BQ�ij��ֱ���������Ȼ�����![]() �Լ���B=��B֤������
�Լ���B=��B֤������
��2���������⣬һ�������������������BPQ�ס�BDA���BQP�ס�BDA��Ȼ�����ô���ʽ��������������BP��BQ��ֵ���������������Ƶ����ʽ������̼��㼴��
��1����t=2ʱ��BP=![]() ��BQ=
��BQ=![]()
��![]() =
=![]()
�֡ߡ�B=��B
����ABC�ס�PBQ
(2)��![]() ʱ��BP=2t��DQ=t
ʱ��BP=2t��DQ=t
��D��BC�е㣬BC=12
��BD=DC=6
��BQ=6-t
����BPQ�ס�BDAʱ��
����![]()
��BP=2t��BD=6,BQ=6-t,BA=10
��![]()
���![]()
����BQP�ס�BDAʱ��
����![]()
��BP=2t��BD=6,BQ=6-t,BA=10
��![]()
���![]()
�൱![]() ʱ��
ʱ��![]() s��
s��![]() sʱ����BQP���BDA����
sʱ����BQP���BDA����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������������A��B��O���㣬����ã�3��3����ʾ����ֽ��A���λ�ã���1��1����ʾB���λ�ã�O��Ҳ��������ϣ�
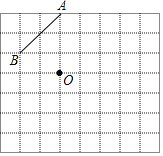
��1��������B����ֱ��OA����ԳƵ�C��д����C���꣮����д��������Ҫ��ͼ�б����ĸ����
��2��������ABC���ڵ�O�����ĶԳ�ͼ�Ρ�A��B��C�䣬д��A�䡢B�䡢C����������ꣻ����д��������Ҫ�����ĸ����
��3���������ϵ���С�����α߳�Ϊ1�������A��B��C��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
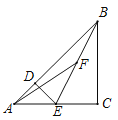
����Ŀ����֪��![]() �͡�
�͡�![]() ���ǵ���ֱ�������Σ�
���ǵ���ֱ�������Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ���е㣮������
���е㣮������![]() �Ƶ�
�Ƶ�![]() ��תһ�ܣ����߶�
��תһ�ܣ����߶�![]() ���ȵ�ȡֵ��Χ�ǣ�������
���ȵ�ȡֵ��Χ�ǣ�������
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����������ΰ���Ƥ����ABC��������AB��10cm���ױ�BC��12cm��
��1��ԲԲͬѧ����вó�����Բ������������Բ�İ뾶��
��2������ͬѧ����вó����������Σ����������������εı߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ཻ��
��ͼ���ཻ��![]() ��
��![]() ���㣬���е�
���㣬���е�![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() .
.
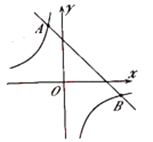
��1������ͼ��ֱ��д������![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���������������ı���ʽ��
��3����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
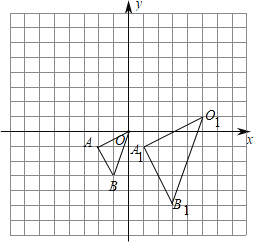
����Ŀ������ͼ��ʾ�ķ����У���OAB�Ķ�������ֱ�ΪO��0��0����A����2����1����B����1����3������O1A1B1���OAB�ǹ��ڵ�PΪλ�����ĵ�λ��ͼ�Σ�
��1����ͼ�б��λ������P��λ�ã���д����P�����꼰��O1A1B1���OAB�����Ʊȣ�
��2����ԭ��OΪλ�����ģ���y���������OAB����һ��λ�ơ�OA2B2��ʹ�����OAB�����Ʊ�Ϊ2��1����д����B�Ķ�Ӧ��B2�����꣮
��3����OA2B2��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����κ�����������������
�ٺ���ͼ����x��Ľ�������ֱ�ΪA��1��0����B��x2��y2������B�ڵ�A���Ҳࣩ��
�ڶԳ�����x=3��
�۸ú�������Сֵ�ǩ�2��
��1�������������Ϣ������κ�������ʽ��
��2�����ú���ͼ��x��x2�IJ���ͼ�����·�����ԭͼ��δ���۵IJ������ͼ����G����ƽ����x���ֱ����ͼ����G���ཻ�ڵ�C��x3��y3����D��x4��y4����E��x5��y5����x3��x4��x5������ϻ����ĺ���ͼ����x3+x4+x5��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��
��1������ú���ͼ��Ķ������꣬�Գ��ᣬͼ����![]() �ᡢ
�ᡢ![]() ��Ľ������ꣻ
��Ľ������ꣻ
��2��![]() ��ʲô��Χ��ʱ��
��ʲô��Χ��ʱ��![]() ��
��![]() �����������
�����������![]() ��ʲô��Χ��ʱ��
��ʲô��Χ��ʱ��![]() ��
��![]() �����������
�����������
��3����![]() ��ʲô��Χ��ʱ��
��ʲô��Χ��ʱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0��b��cΪ��������ͼ����ͼ��ʾ������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����3b��2c����a+b��m��am+b����mΪ��������m��1����������ȷ�Ľ�����_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com