
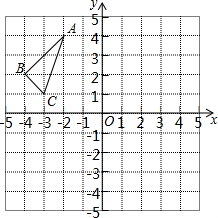
 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.科目:初中数学 来源: 题型:选择题
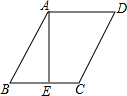 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )| A. | $12-6\sqrt{2}$ | B. | $6\sqrt{2}+12$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:解答题
抛物线经过A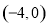 ,B
,B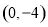 ,C
,C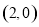 三点.
三点.
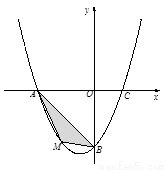
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线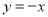 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50名学生 | B. | 50名学生的身高 | C. | 400名学生 | D. | 400名学生的身高 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4,0) | B. | (6,0) | C. | (-4,0)或(6,0) | D. | (0,12)或(0,-8) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.
如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com